(本小题满分13分)椭圆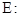
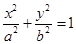 (
( )的左焦点为
)的左焦点为 ,右焦点为
,右焦点为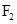 ,离心率
,离心率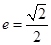 .设动直线
.设动直线
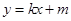 与椭圆
与椭圆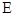 相切于点
相切于点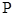 且交直线
且交直线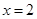 于点
于点 ,
,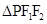 的周长为
的周长为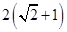 .
.
(1)求椭圆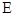 的方程;
的方程;
(2)求两焦点 、
、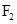 到切线
到切线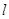 的距离之积;
的距离之积;
(3)求证:以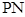 为直径的圆恒过点
为直径的圆恒过点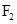
已知二次函数f(x)=x2+ax(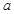
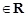 ).
).
(1)若函数y=f(sinx+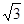 cosx)(
cosx)(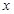
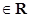 )的最大值为
)的最大值为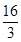 ,求f(x)的最小值;
,求f(x)的最小值;
(2)当a>2时,求证:f(sin2xlog2sin2x+cos2xlog2cos2x)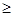 1–a.其中x∈R,x¹kp且x¹kp
1–a.其中x∈R,x¹kp且x¹kp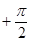 (k∈Z).
(k∈Z).
已知函数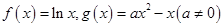 .
.
(1)若函数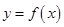 与
与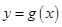 的图象在公共点P处有相同的切线,求实数
的图象在公共点P处有相同的切线,求实数 的值及点P的坐标;
的值及点P的坐标;
(2)若函数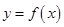 与
与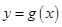 的图象有两个不同的交点M、N,求实数
的图象有两个不同的交点M、N,求实数 的取值范围 .
的取值范围 .
在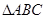 中,满足:
中,满足: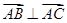 ,
,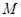 是
是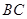 的中点.
的中点.
(1)若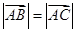 ,求向量
,求向量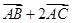 与向量
与向量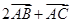 的夹角的余弦值;
的夹角的余弦值;
(2)若点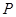 是
是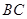 边上一点,
边上一点,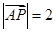 ,且
,且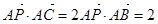 ,求
,求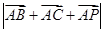 的最小值.
的最小值.
如图,在直角坐标系xOy中,锐角△ABC内接于圆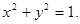 已知BC平行于x轴,AB所在直线方程为
已知BC平行于x轴,AB所在直线方程为 ,记角A,B,C所对的边分别是a,b,c.
,记角A,B,C所对的边分别是a,b,c.
(1)若 的值;
的值;
(2)若 的值.
的值.
已知向量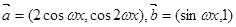 (
( ),
), 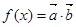 ,且
,且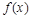 的周期为
的周期为 .
.
(1)求f( )的值;
)的值;
(2)写出f(x)在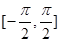 上的单调递增区间.
上的单调递增区间.