(本小题满分14分)已知曲线 上的一个最高点的坐标为
上的一个最高点的坐标为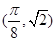 ,则此点到相邻最低点间的曲线与
,则此点到相邻最低点间的曲线与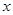 轴交于点(
轴交于点(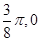 ),若
),若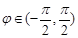 .
.
(1)试求这条曲线的函数表达式;
(2)用“五点法”画出(1)中函数在 上的图像.
上的图像.
如图,在直三棱柱ABC-A1B1C1中,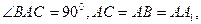 E是BC的中点。
E是BC的中点。
(1)求异面直线AE与A1C所成的角;
(2)若G为C1C上一点,且EG⊥A1C,试确定点G的位置;
|
(3)在(2)的条件下,求二面角A1-AG-E的大小
为预防 病毒暴发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没
病毒暴发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没 有通过),公司选定2000个流感样本分成三组,测试结果如下表:
有通过),公司选定2000个流感样本分成三组,测试结果如下表:
| A组 |
B组 |
C组 |
|
| 疫苗有效 |
673 |
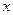 |
 |
| 疫苗无效 |
77 |
90 |
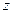 |
已知在全体样本中随机抽取1个,抽到B组疫苗有效的概率是0.33.
(1)求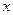 的值;
的值;
(2)现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C组抽取多少个?
(3)已知 ,求不能通过测试的概率.
,求不能通过测试的概率.
已知向量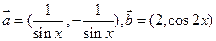 ,其中
,其中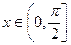 .
.
(1)试判断向量 与
与 能否平行,并说明理由?
能否平行,并说明理由?
(2)求函数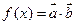 的最小值.
的最小值.
(本小题满分12分)
设函数
(Ⅰ)若函 数
数 在其定义域内是增函数,求
在其定义域内是增函数,求 的取值范围;
的取值范围;
(Ⅱ)设 ,方程
,方程 有两根
有两根 ,记
,记 .试探究
.试探究 值的符号,其中
值的符号,其中 是
是 的导函数.
的导函数.
(本小题满分12分)
已知点 和直线
和直线 ,作
,作 垂足为Q,且
垂足为Q,且
(Ⅰ)求点P的轨迹方程;
(Ⅱ)过点C的直线 与点P轨迹交于两点
与点P轨迹交于两点 ,
, ,点
,点 ,若
,若 的面积为
的面积为 ,求直线
,求直线 的方程.
的方程.