已知直线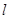 :y="k" (x+2
:y="k" (x+2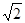 )与圆O:
)与圆O: 相交于A、B两点,O是坐标原点,
相交于A、B两点,O是坐标原点,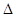 ABO的面积为S.
ABO的面积为S.
(1)试将S表示成的函数S(k),并求出它的定义域;
(2)求S的最大值,并求取得最大值时k的值.
((本小题满分12分)
如图,几何体ABCDE中,△ABC是正三角形,EA和DC都垂直于平面ABC,且EA=AB=2a, DC=a,F、G分别为EB和AB的中点.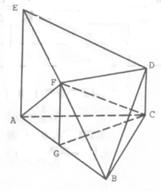
(1)求证:FD∥平面ABC;
(2)求证:AF⊥BD;
(3) 求二面角B—FC—G的正切值.
((本小题满分12分)
如图,斜三棱柱 -ABC的底面是边长为2的正三角形,顶点
-ABC的底面是边长为2的正三角形,顶点 在底面上的射影是△ABC的中心,
在底面上的射影是△ABC的中心,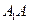 与AB的夹角是45°
与AB的夹角是45°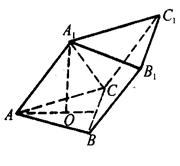
( 1)求证:
1)求证: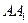 ⊥平面
⊥平面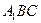 ;
;
(2)求此棱柱的侧面积 。
( (本小题满分12分)
在棱长为4的正方体ABCD-A1B1C1D1中,O是正方形A1B1C1D1的中心,点P在棱CC1上,且CC1=4CP.
(1)、求直线AP与平面BCC1B1所成的角的大小(结果用反三角函数值表示);
(2)、求点P到平面ABD1的距离.
(本小题满分12分)
如图,在三棱锥P-ABC中,PA=PC,∠APC=∠ACB=90°,∠BAC=30°,平面PAC⊥平面ABC.
(1)求证:平面PAB⊥平面PBC;
(2)若PA=2,求三棱锥P-ABC的体积.
(本小题满分10分)
7名学生站成一排,下列情况各有多少种不同的排法?
(1)甲、乙必须排在一起;
(2)甲不在排头,乙不在排尾;
(3)甲、乙互不相邻;
(4)甲、乙之间须隔一人