我们在配平化学方程式时，对于某些简单的方程式可以用观察法配平，对于某些复杂的方程式，还可以尝试运用方程的思想和比例的方法．例如方程式：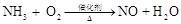
，可以设NH3的系数为1，其余三项系数分别为x、y、z，即：
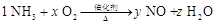，依据反应前后各元素守恒，得：
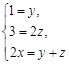，解之得四项系数之比为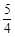1:
:1: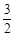
，扩大4倍得整数比为4:5:4:6，即配平结果为：
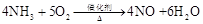．请运用上述方法，配平化学方程式：
．
， ．
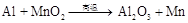计算： ．
在几何体表面上，蚂蚁怎样爬行路径最短？
（1）如图①，圆锥的母线长为 ， 为母线 的中点，点 在底面圆周上， 的长为 ．在图②所示的圆锥的侧面展开图中画出蚂蚁从点 爬行到点 的最短路径，并标出它的长（结果保留根号）．
（2）图③中的几何体由底面半径相同的圆锥和圆柱组成． 是圆锥的顶点，点 在圆柱的底面圆周上，设圆锥的母线长为 ，圆柱的高为 ．
①蚂蚁从点 爬行到点 的最短路径的长为 （用含 ， 的代数式表示）．
②设 的长为 ，点 在母线 上， ．圆柱的侧面展开图如图④所示，在图中画出蚂蚁从点 爬行到点 的最短路径的示意图，并写出求最短路径的长的思路．
已知二次函数 的图象经过 ， 两点．
（1）求 的值；
（2）当 时，该函数的图象的顶点的纵坐标的最小值是 1 ．
（3）设 是该函数的图象与 轴的一个公共点．当 时，结合函数的图象，直接写出 的取值范围．
如图，已知 是 外一点．用两种不同的方法过点 作 的一条切线．
要求：（1）用直尺和圆规作图；
（2）保留作图的痕迹，写出必要的文字说明．
