如图，将□OABC放置在平面直角坐标系xOy内，已知AB边所在直线的解析为：y = − x + 4．点C的坐标是（ ▲ ， ▲ ）
若将□OABC绕点O逆时针旋转90°得OBDE，BD交OC于点P，求△OBP的面积；
在(2)的情形下，若再将四边形OBDE沿y轴正方向平移，设平移的距离为x（0≤x≤8），与□OABC重叠部分面积为S，试写出S关于x的函数关系式，并求出S的最大值．
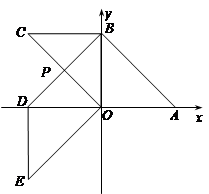
如图，⊙O的直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，求BC，AD，BD的长．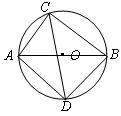
如图，在Rt△ABC中，∠ACB=90°，∠B =60°，BC=2．点O是AC的中点，过点O的直线l从与AC重合的位置开始，绕点O作逆时针旋转，交AB边于点D．过点C作CE∥AB交直线l于点E，设直线l的旋转角为α．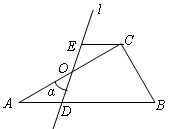
（1）①当α=________度时，四边形EDBC是等腰梯形，此时AD的长为_________；
②当α=________度时，四边形EDBC是直角梯形，此时AD的长为_________；
（2）当α=90°时，判断四边形EDBC是否为菱形，并说明理由．
要对一块长60m、宽40m的矩形荒地ABCD进行绿化和硬化．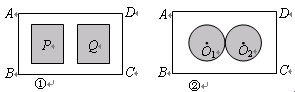
（1）设计方案如图①所示，矩形P、Q为两块绿地，其余为硬化路面，P、Q两块绿地周围的硬化路面宽都相等，并使两块绿地面积的和为矩形ABCD面积的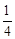
，求P、Q两块绿地周围的硬化路面的宽．
（2）某同学有如下设想：设计绿化区域为相外切的两等圆，圆心分别为O1和O2，且O1到AB，BC，AD的距离与O2到CD，BC，AD的距离都相等，其余为硬化地面，如图②所示，这个设想是否成立？若成立，求出圆的半径；若不成立，说明理由．
解方程：x2＋2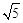
x―4=0．
解方程：（1）x2＋x―12=0；