为了解某班学生喜欢打篮球是否与性别有关，对本班50人进行了问卷调查得到了下表：
| 喜爱打篮球 |
不喜爱打篮球 |
合计 |
|
| 男生 |
20 |
5 |
25 |
| 女生 |
10 |
15[ |
25 |
| 合计 |
30 |
20 |
50 |
下面的临界值表供参考：
| P(K2≥k0) |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k0 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
则根据以下参考公式可得随机变量K2的值为 (保留三位小数)，有 %的把握认为喜爱打篮球与性别有关．(参考公式：K2＝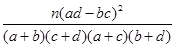
，其中n＝a＋b＋c＋d)
设m∈R，过定点A的动直线x+my=0和过定点B的直线mx﹣y﹣m+3=0交于点P（x，y），则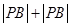 
的最大值是 。
如图是一个几何体的三视图，该几何体的体积是 ．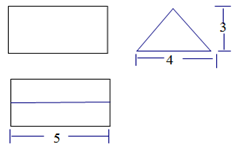
不等式﹣x2﹣2x+3＜0的解集为 ．
若存在实常数
和
，使得函数
和
对其公共定义域上的任意实数
都满足：
和
恒成立，则称此直线
为和的“隔离直线”，已知函数
，
，
，有下列命题：
①
在
内单调递增；
②
和
之间存在“隔离直线”，且的最小值为
；
③和之间存在“隔离直线”，且的取值范围是
；·
④和
之间存在唯一的“隔离直线”
．
其中真命题的个数为 （请填所有正确命题的序号）
利用一个球体毛坯切削后得到一个四棱锥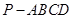
,其中底面四边形是边长为
的正方形，
，且
平面
,则球体毛坯体积的最小值应为 ．