(本小题12分)已知函数 的图象在
的图象在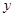 轴上的截距为1,在相邻两最值点
轴上的截距为1,在相邻两最值点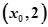 ,
,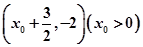 上
上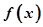 分别取得最大值和最小值.
分别取得最大值和最小值.
⑴求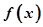 的解析式;
的解析式;
⑵若函数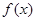 满足方程
满足方程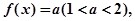 求在
求在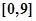 内的所有实数根之和.
内的所有实数根之和.
已知函数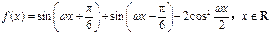 (其中
(其中
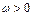 )
)
(1)求函数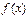 的值域;
的值域;
(2)若函数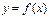 的图象与直线
的图象与直线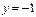 的两个相邻交点间的距离为
的两个相邻交点间的距离为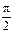 ,求函数
,求函数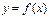 的单调增区间.
的单调增区间.
已知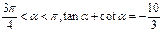 ,
,
(1)求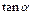 的值;
的值;
(2)求 的值.
的值.
(本小题满分12分)
已知数列{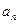 }中,
}中, (n≥2,
(n≥2,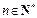 ),
),
(1)若 ,数列
,数列 满足
满足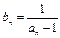 (
(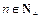 ),求证数列{
),求证数列{ }是等差数列;
}是等差数列;
(2)若 ,求数列{
,求数列{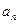 }中的最大项与最小项,并说明理由;
}中的最大项与最小项,并说明理由;
(3)(理做文不做)若 ,试证明:
,试证明: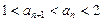 .
.
(本小题满分12分)
某市某通讯设备厂为适应市场需求,提高效益,特投入98万元引进世界先进设备奔月8号,并马上投入生产.第一年需要的各种费用是12万元,从第二年开始,所需费用会比上一年增加4万元,而每年因引入该设备可获得的年利润为50万元.
请你根据以上数据,解决下列问题:
(1)引进该设备多
 少年后,开始盈利?
少年后,开始盈利?
(2) 引进该设备若干年后,有两种处理方案:
引进该设备若干年后,有两种处理方案:
第一种:年平均盈利达到最大值时,以26万元的价格卖出;
第二种:盈利总额达到最大值时,以8万元的价格卖出.
问哪种方案较为合算?并说明理由.
(本小题满分12分)
某市2006年底有住房面积1200万平方米,计划从2007年起,每年拆除20万平方米的旧住房.假定该市每年新建住房面积是上年年底住房面积的5%.
(1)分别求2007年底和2008年底的住房面积;
(2)求2026年底的住房面积.(计算结果以万平方米为单位,且精确到0.01)