某射手在一次射击训练中,射中10环、9环、8环、7环的概率分别为0.21,0.23,0.25,0.28,计算该射手在一次射击中:
(1)射中10环或9环的概率;
(2)少于7环的概率。
在直三棱柱 中,
中, ,
, ,求:
,求:
(1)异面直线 与
与 所成角的大小;
所成角的大小;
(2)四棱锥 的体积.
的体积.
在等差数列 和等比数列
和等比数列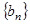 中,
中,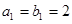 ,
,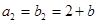 ,
,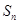 是
是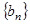 前
前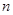 项和.
项和.
(1)若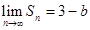 ,求实数
,求实数 的值;
的值;
(2)是否存在正整数 ,使得数列
,使得数列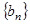 的所有项都在数列
的所有项都在数列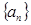 中?若存在,求出所有的
中?若存在,求出所有的 ,若不存在,说明理由;
,若不存在,说明理由;
(3)是否存在正实数 ,使得数列
,使得数列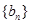 中至少有三项在数列
中至少有三项在数列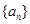 中,但
中,但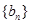 中的项不都在数列
中的项不都在数列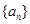 中?若存在,求出一个可能的
中?若存在,求出一个可能的 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
已知点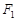 、
、 为双曲线
为双曲线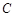 :
: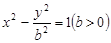 的左、右焦点,过
的左、右焦点,过 作垂直于
作垂直于 轴的直线,在
轴的直线,在 轴上方交双曲线
轴上方交双曲线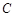 于点
于点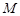 ,且
,且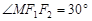 .圆
.圆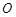 的方程是
的方程是 .
.
(1)求双曲线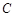 的方程;
的方程;
(2)过双曲线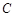 上任意一点
上任意一点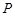 作该双曲线两条渐近线的垂线,垂足分别为
作该双曲线两条渐近线的垂线,垂足分别为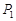 、
、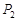 ,求
,求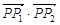 的值;
的值;
(3)过圆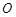 上任意一点
上任意一点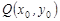 作圆
作圆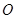 的切线
的切线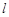 交双曲线
交双曲线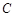 于
于 、
、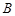 两点,
两点,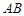 中点为
中点为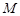 ,求证:
,求证: .
.
如图,制图工程师要用两个同中心的边长均为4的正方形合成一个八角形图形.由对称性,图中8个三角形都是全等的三角形,设 .
.
(1)试用 表示
表示 的面积;
的面积;
(2)求八角形所覆盖面积的最大值,并指出此时 的大小.
的大小.
已知 ,其中
,其中 是常数.
是常数.
(1)若 是奇函数,求
是奇函数,求 的值;
的值;
(2)求证: 的图像上不存在两点A、B,使得直线AB平行于
的图像上不存在两点A、B,使得直线AB平行于 轴.
轴.