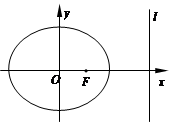已知函数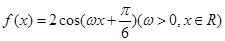 的最小正周期为
的最小正周期为 .
.
⑴求函数 的对称轴方程;⑵设
的对称轴方程;⑵设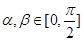 ,
, ,求
,求 的值.
的值.
已知 ,命题
,命题 ,命题
,命题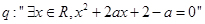 .⑴若命题
.⑴若命题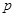 为真命题,求实数
为真命题,求实数 的取值范围;⑵若命题
的取值范围;⑵若命题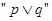 为真命题,命题
为真命题,命题 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.
已知椭圆G: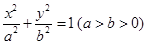 过点
过点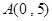 ,
, ,C、D在该椭圆上,直线CD过原点O,且在线段AB的右下侧.
,C、D在该椭圆上,直线CD过原点O,且在线段AB的右下侧.
(1)求椭圆G的方程;
(2)求四边形ABCD 的面积的最大值.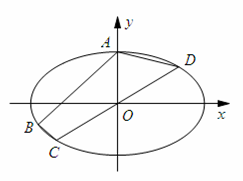
已知圆M的圆心在直线 上,且过点
上,且过点 、
、 .
.
(1)求圆M的方程;
(2)设P为圆M上任一点,过点P向圆O: 引切线,切点为Q.试探究:
引切线,切点为Q.试探究:
平面内是否存在一定点R,使得 为定值?若存在,求出点R的坐标;若不存在,请说
为定值?若存在,求出点R的坐标;若不存在,请说
明理由.
如图,F是中心在原点、焦点在x轴上的椭圆C的右焦点,直线l:x=4是椭圆C的右准线,F到直线l的距离等于3.
(1)求椭圆C的方程;
(2)点P是椭圆C上动点,PM⊥l,垂足为M.是否存在点P,使得△FPM为等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.