如图1,在中,,,,分别是上的点,且,,将沿折起到的位置,使,如图2.
(1)求证:平面;
(2)若是的中点,求与平面所成角的大小;
(3)线段上是否存在点,使平面与平面垂直?说明理由
设函数f(x)="|2x-1|+|2x-3|" , x∈R.
(Ⅰ)解不等式f(x)≤5;
(Ⅱ)若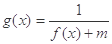 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围.
在平面直角坐标系中,直线 的参数方程为
的参数方程为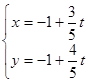 (
(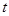 为参数).若以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为
为参数).若以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为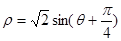 .
.
(Ⅰ) 求曲线C的直角坐标方程;
(Ⅱ) 求直线 被曲线
被曲线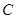 所截得的弦长.
所截得的弦长.
如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且DE2 = EF·EC.
(Ⅰ)求证:CE·EB = EF·EP;
(Ⅱ)若CE:BE = 3:2,DE = 3,EF = 2,求PA的长.
已知函数 .
.
(Ⅰ)函数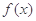 在区间
在区间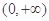 上是增函数还是减函数?证明你的结论;
上是增函数还是减函数?证明你的结论;
(Ⅱ)当 时,
时, 恒成立,求整数
恒成立,求整数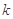 的最大值;
的最大值;
(Ⅲ)试证明: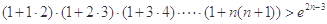 .
.
如图,已知椭圆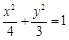 的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.
的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.
(Ⅰ)若点G的横坐标为 ,求直线AB的斜率;
,求直线AB的斜率;
(Ⅱ)记△GFD的面积为S1,△OED(O为原点)的面积为S2.
试问:是否存在直线AB,使得S1=S2?说明理由.