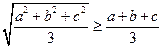已知函数
(
为常数,
是自然对数的底数),曲线
在点
处的切线与
轴平行.
(Ⅰ)求
的值;
(Ⅱ)求
的单调区间;
(Ⅲ)设
,其中
为
的导函数.证明:对任意
.
为了让学生了解更多“社会法律”知识,
| 分组 |
频数 |
频率 |
| 60.5~70.5 |
1 |
0.16 |
| 70.5~80.5 |
10 |
2 |
| 80.5~90.5 |
18 |
0.36 |
| 90.5~100.5 |
3 |
4 |
| 合计 |
50 |
1 |
某中学举行了一次“社会法律知识竞赛”,
共有800名学生参加了这次竞赛. 为了解
本次竞赛成绩情况,从中抽取了部分学
生的成绩(得分均为整数,满分为100
分)进行统计.请你根据尚未完成并有
局部污损的频率分布表,解答下列问题:
(1)若用系统抽样的方法抽取50个样本,
现将所有学生随机地编号为000,001,002,…,799,试写出第二组第一位学生的编号 ;
(2)填充频率分布表的空格1 2 3 4 并作出频率分布直方图;
(3)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约有多少人?
记集合 ,
,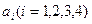 是
是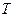 中可重复选取的元素.
中可重复选取的元素.
(1)若将集合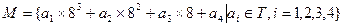 中所有元素按从小到大的顺序排列,求第2008个数所对应的
中所有元素按从小到大的顺序排列,求第2008个数所对应的 的值;
的值;
(2)若将集合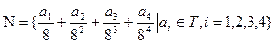 中所有元素按从大到小的顺序排列,求第2008个数所对应的
中所有元素按从大到小的顺序排列,求第2008个数所对应的 的值.
的值.
设有2009个人站成一排,从第一名开始1至3报数,凡报到3的就退出队伍,其余的向前靠拢站成新的一排,再按此规则继续进行,直到第p次报数后只剩下3人为止,试问最后剩下3人最初在什么位置?
.已知矩阵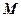
 ,其中
,其中 ,若点
,若点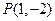 在矩阵
在矩阵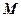 的变换下得到点
的变换下得到点 ,
,
(1)求实数a的值;
(2)求矩阵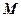 的特征值及其对应的特征向量.
的特征值及其对应的特征向量.
求证: