在极坐标系中,求方程ρ=4cos(θ+ )的普通方程以及表示的曲线?
)的普通方程以及表示的曲线?
(本小题满分12分)在10件产品中,有8件是合格的,2件是次品,从中任意抽2件进行检验.
计算:(1)两件都是次品的概率;
(2)2件中恰好有一件是合格品的概率;
(3)至多有一件是合格品的概率.
(本小题满分12分)
已知椭圆的中心在坐标原点 ,焦点在
,焦点在 轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,短轴长为2.
轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,短轴长为2.
(1)求椭圆的方程;
(2)设直线 过
过 且与椭圆相交于A,B两点,当P是AB的中点时,求直线
且与椭圆相交于A,B两点,当P是AB的中点时,求直线 的方程.
的方程.
(本小题满分12分)已知:过抛物线 的焦点
的焦点 的直线交抛物线于
的直线交抛物线于 两点。
两点。
求证:(1) 为定值;
为定值;
(2) 为定值.
为定值.
(本小题满分10分)给定两个命题, :对任意实数
:对任意实数 都有
都有 恒成立;
恒成立; :关于
:关于 的方程
的方程 有实数根;如果
有实数根;如果 与
与 中有且仅有一个为真命题,求实数
中有且仅有一个为真命题,求实数 的取值范围.
的取值范围.
(本小题满分12分)
设 为实数,函数
为实数,函数 .
.
(1)若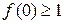 ,求
,求 的取值范围;
的取值范围;
(2)求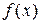 的最小值;
的最小值;
(3)设函数 ,直接写出(不需给出演算步骤)不等式
,直接写出(不需给出演算步骤)不等式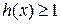 的解集.
的解集.