为响应市教育局倡导的“阳光体育运动”的号召,全校学生积极参与体育运动.为了进一步了解学校九年级学生的身体素质情况,体育老师在九年级800名学生中随机抽取50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下所示:
请结合图表完成下列问题:
(1)表中的 ;
;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第 组;
(4) 若九年级学生一分钟跳绳次数( )达标要求是:
)达标要求是: 为不合格;
为不合格;
为合格; 为良;
为良; 为优.根据以上信息,请你估算学校九年级同学一分钟跳绳次数为优的人数为 .
为优.根据以上信息,请你估算学校九年级同学一分钟跳绳次数为优的人数为 .
实验中学现有学生2870人,学校为了进一步丰富学生课余生活,拟调查各兴趣小组活动情况,为此校学生会委托小容、小易进行一次随机抽样调查.根据采集到的数据,小容绘制的统计图1,小易绘制的统计图2(不完整)如下:
请你根据统计图1、2中提供的信息,解答下列问题:写出2条有价值信息(不包括下面要计算的信息);
这次抽样调查的样本容量是多少?在图2中,请将小易画的统计图中的“体育”部分的图形补充完整;
爱好“书画”的人数占被调查人数的百分数是多少?估计实验中学现有的学生中,有多少人爱好“书画”?
小明到某品牌服装专卖店做社会调查.了解到该专卖店为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,而“计件奖金=销售每件的奖金×月销售件数”,并获得如下信息:
| 营业员 |
甲 |
乙 |
| 月销售件数(件) |
200 |
150 |
| 月总收入(元) |
1400 |
1250 |
列方程(组),求营业员的月基本工资和销售每件的奖金;
营业员丙月总收入不低于
 元,这位营业员当月至少要卖服装多少件?
元,这位营业员当月至少要卖服装多少件?
如图,已知: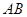 是
是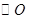 的直径,
的直径,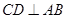 于E,连接AD、OC.
于E,连接AD、OC.证明:
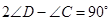 ;
;若
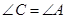 ,求∠D的度数.
,求∠D的度数.
如图,已知:在 中,
中, ,
, ,垂足为点
,垂足为点 ,
, 是
是 外角
外角 的平分线,
的平分线, ,垂足为点
,垂足为点 .
.求证:四边形
 为矩形;
为矩形;当
 满足什么条件时,四边形
满足什么条件时,四边形 是一个正方形?(不必证明).
是一个正方形?(不必证明).
在一个红色不透明的盒子中放有四张分别写有数字1,2,3,4的红色卡片,在一个蓝色不透明的盒子中放有三张分别写有数字1,2,3的蓝色卡片,卡片除颜色和数字外完全相同.从红盒中任意抽取一张红色卡片,从蓝盒中任意抽取一张蓝色卡片,用列举法(树形图或列表法)表示所有的可能情况;
求两张卡片上写有相同数字的概率.