已知正方体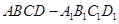 的棱长为1,点
的棱长为1,点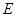 在
在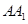 上,点
上,点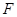 在
在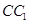 上,且
上,且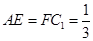
(1)求直线 与平面
与平面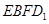 所成角的余弦值;
所成角的余弦值;
(2)用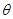 表示平面
表示平面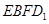 和侧面
和侧面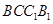 所成的锐二面角的大小,求
所成的锐二面角的大小,求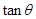 ;
;
(3)若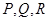 分别在
分别在 上,并满足
上,并满足 ,探索:当
,探索:当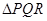 的重心为
的重心为 且
且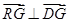 时,求实数
时,求实数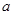 的取值范围.
的取值范围.
如图,四棱柱 中,
中,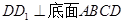 .
.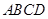 为平行四边形,
为平行四边形,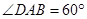 ,
, 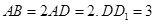 ,
, 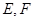 分别是
分别是 与
与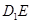 的中点.
的中点.
(1)求证: ;
;
(2)求二面角 的平面角的余弦值.
的平面角的余弦值.
某电视台“挑战60秒”活动规定上台演唱:
(I)连续达到60秒可转动转盘(转盘为八等分圆盘)一次进行抽奖,达到90秒可转两次,达到120秒可转三次(奖金累加).
(2)转盘指针落在I、II、III区依次为一等奖(500元)、二等奖(200元)、三等奖(100元),落在其它区域不奖励.
(3)演唱时间从开始到三位评委中至少1人呜啰为止,现有一演唱者演唱时间为100秒.
①求此人中一等奖的概率;
②设此人所得奖金为 ,求
,求 的分布列及数学期望
的分布列及数学期望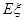 .
.
(13分)已知函数 的图象在点
的图象在点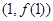 处的切线垂直于
处的切线垂直于 轴.
轴.
(1)求实数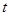 的值;
的值;
(2)求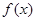 的极值.
的极值.
已知 .
.
(1)求不等式 的解集A;
的解集A;
(2)若不等式 对任何
对任何 恒成立,求
恒成立,求 的取值范围.
的取值范围.
已知数列 的前
的前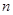 项和为
项和为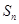 ,且
,且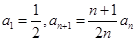 .
.
(1)求 的通项公式;
的通项公式;
(2)设 恰有5个元素,求实数
恰有5个元素,求实数 的取值范围.
的取值范围.