如图，一个小球从M处投入，通过管道自上而下落A或B或C。已知-优题课

题文

如图，一个小球从M处投入，通过管道自上而下落A或B或C。已知小球从每个叉口落入左右两个管道的可能性是相等的．某商家按上述投球方式进行促销活动，若投入的小球落到A，B，C，则分别设为l，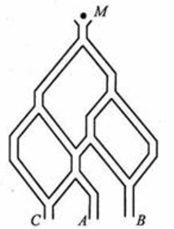

2，3等奖．（I）已知获得l，2，3等奖的折扣率分别为50％，70％，90％．记随变量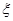为获得k(k=1,2,3)等奖的折扣率，求随机变量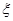的分布列及期望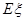；(II)若有3人次(投入l球为l人次)参加促销活动，记随机变量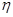为获得1等奖或2等奖的人次，求．

科目数学题型解答题难度中等

知识点：随机思想的发展

登录免费查看答案和解析

相关试题

设函数 $f (x) = \frac{\ln x}{1 + x} - \ln x + \ln (x + 1)$ ．
（Ⅰ）求 $f (x)$ 的单调区间和极值；
（Ⅱ）是否存在实数 $a$ ，使得关于 $x$ 的不等式 $f (x) \geq a$ 的解集为（0，+ $\infty$ ）？若存在，求 $a$ 的取值范围；若不存在，试说明理由．

在数列 $\{a_{n}\}$ ， $\{b_{n}\}$ 中， $a_{1} = 2, b_{1} = 4$ ，且 $a_{n}, b_{n}, a_{n + 1}$ 成等差数列， $b_{n}, a_{n + 1}, b_{n + 1}$ 成等比数列（ $n \in N^{*}$ ）
（Ⅰ）求 $a_{2}, a_{3}, a_{4}$ 及 $b_{2}, b_{3}, b_{4}$ ，由此猜测 $\{a_{n}\}$ ， $\{b_{n}\}$ 的通项公式，并证明你的结论；
（Ⅱ）证明： $\frac{1}{a_{1} + b_{1}} + \frac{1}{a_{2} + b_{2}} + . . . + \frac{1}{a_{n} + b_{n}} < \frac{5}{12}$ ．

在直角坐标系 $x O y$ 中，点 $P$ 到两点 $(0, - \sqrt{3}), (0, \sqrt{3})$ 的距离之和等于4，设点 $P$ 的轨迹为 $C$ ，直线 $y = k x + 1$ 与 $C$ 交于 $A, B$ 两点．
（Ⅰ）写出 $C$ 的方程；
（Ⅱ）若 $\overset{⇀}{O A} ⊥ \overset{⇀}{O B}$ ，求 $k$ 的值；
（Ⅲ）若点 $A$ 在第一象限，证明：当 $k > 0$ 时，恒有 $|\overset{⇀}{O A}| > |\overset{⇀}{O B}|$ ．

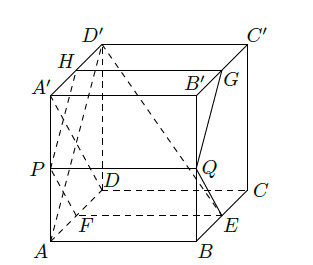
如图，在棱长为1的正方体 $A B C D - A^{`} B^{`} C^{`} D^{`}$ 中， $A P = B Q = b (0 < b < 1)$ ，截面 $P Q E F ∥ A^{`} D$ ，截面 $P Q G H ∥ A D^{`}$ ．

（Ⅰ）证明：平面 $P Q E F$ 和平面 $P Q G H$ 互相垂直；
（Ⅱ）证明：截面 $P Q E F$ 和截面 $P Q G H$ 面积之和是定值，
并求出这个值；
（Ⅲ）若 $D^{`} E$ 与平面 $P Q E F$ 所成的角为 $45^{°}$ ，求 $D^{`} E$ 与平
面 $P Q E F$ 所成角的正弦值．

某批发市场对某种商品的周销售量（单位：吨）进行统计，最近100周的统计结果如下表所示：

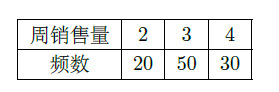
（Ⅰ）根据上面统计结果，求周销售量分别为2吨，3吨和4吨的频率；
（Ⅱ）已知每吨该商品的销售利润为2千元， $ξ$ 表示该种商品两周销售利润的和(单位：千元).若以上述频率作为概率，且各周的销售量相互独立，求 $ξ$ 的分布列和数学期望．

试卷网试题网古诗词网作文网范文网

Copyright ©2020-2025 优题课 youtike.com 版权所有

粤ICP备20024846号