(1)已知函数f(x)=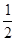 x
x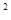 -ax+(a-1)
-ax+(a-1)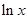 ,
,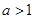 。讨论函数
。讨论函数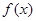 的单调性;
的单调性;
(2).已知函数f (x)=lnx,g(x)=ex.设直线l为函数 y=f (x) 的图象上一点A(x0,f (x0))处的切线.问在区间(1,+∞)上是否存在x0,使得直线l与曲线y=g(x)也相切.若存在,这样的x0有几个?,若没有,则说明理由。
已知中心在原点,左、右顶点A1、A2在x轴上,离心率为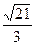 的双曲线C经过点P(6,6),动直线l经过△A1PA2的重心G与双曲线C交于不同两点M、N,Q为线段MN的中点。
的双曲线C经过点P(6,6),动直线l经过△A1PA2的重心G与双曲线C交于不同两点M、N,Q为线段MN的中点。
(1)求双曲线C的标准方程
(2)当直线l的斜率为何值时,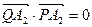 。
。
已知椭圆 的离心率为,且其焦点F(c,0)(c>0)到相应准线l的距离为3,过焦点F的直线与椭圆交于A、B两点。
的离心率为,且其焦点F(c,0)(c>0)到相应准线l的距离为3,过焦点F的直线与椭圆交于A、B两点。
(1)求椭圆的标准方程;
(2)设M为右顶点,则直线AM、BM与准线l分别交于P、Q两点,(P、Q两点不重合),求证:
在面积为9的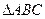 中,
中, ,且
,且 。现建立以A点为坐标原点,以
。现建立以A点为坐标原点,以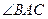 的平分线所在直线为x轴的平面直角坐标系,如图所示。
的平分线所在直线为x轴的平面直角坐标系,如图所示。
(1)求AB、AC所在的直线方程;
(2)求以AB、AC所在的直线为渐近线且过点D的双曲线的方程;
(3)过D分别作AB、AC所在直线的垂线DF、DE(E、F为垂足),求 的值。
的值。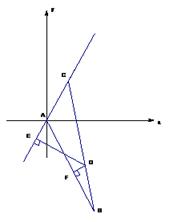
如图,椭圆的中心在原点,其左焦点 与抛物线
与抛物线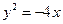 的焦点重合,过
的焦点重合,过 的直线
的直线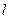 与椭圆交于A、B两点,与抛物线交于C、D两点.当直线
与椭圆交于A、B两点,与抛物线交于C、D两点.当直线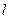 与x轴垂直时,
与x轴垂直时,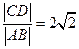 .
.
(Ⅰ)求椭圆的方程;
(II)求过点O、 ,并且与椭圆的左准线相切的圆的方程;
,并且与椭圆的左准线相切的圆的方程;
(Ⅲ)求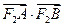 的最大值和最小值.
的最大值和最小值.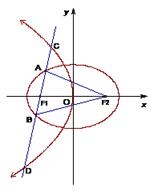
已知点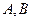 分别是射线
分别是射线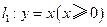 ,
,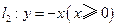 上的动点,
上的动点,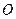 为坐标原点,且
为坐标原点,且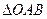 的面积为定值2.
的面积为定值2.
(I)求线段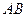 中点
中点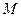 的轨迹
的轨迹 的方程;
的方程;
(II)过点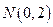 作直线
作直线 ,与曲线
,与曲线 交于不同的两点
交于不同的两点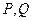 ,与射线
,与射线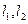 分别交于点
分别交于点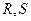 ,若点
,若点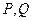 恰为线段
恰为线段 的两个三等分点,求此时直线
的两个三等分点,求此时直线 的方程.
的方程.