已知定义在R上的函数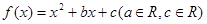 ,
,
定义: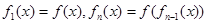 .
.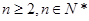
(1)若 ,当
,当 时比较
时比较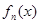 与
与 的大小关系.
的大小关系.
(2)若对任意的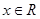 ,都有使得
,都有使得 ,用反证法证明:
,用反证法证明: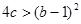 .
.
已知数列 满足
满足 ,
,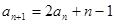
(1)求证:数列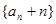 是等比数列;
是等比数列;
(2)求数列 的通项和前n项和
的通项和前n项和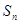 .
.
已知向量 ,且
,且 ,A为锐角,求:
,A为锐角,求:
(1)角A的大小;
(2)求函数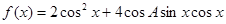 的单调递增区间和值域.
的单调递增区间和值域.
已知函数 和
和 的定义域分别是集合A、B,
的定义域分别是集合A、B,
(1)求集合A,B;
(2)求集合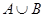 ,
, .
.
如图, 是△
是△ 的重心,
的重心,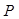 、
、 分别是边
分别是边 、
、 上的动点,且
上的动点,且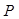 、
、 、
、 三点共线.
三点共线.
(1)设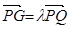 ,将
,将 用
用 、
、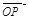 、
、 表示;
表示;
(2)设 ,
, ,证明:
,证明: 是定值;
是定值;
(3)记△ 与△
与△ 的面积分别为
的面积分别为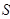 、
、 .求
.求 的取值范围.
的取值范围.
(提示:

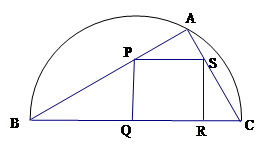
如图,某小区准备绿化一块直径为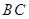 的半圆形空地,
的半圆形空地, 外的地方种草,
外的地方种草, 的内接正方形
的内接正方形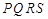 为一水池,其余地方种花.若
为一水池,其余地方种花.若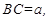
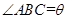 ,设
,设 的面积为
的面积为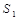 ,正方形
,正方形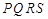 的面积为
的面积为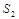 ,将比值
,将比值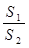 称为“规划合理度”.
称为“规划合理度”.
(1)试用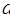 ,
,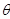 表示
表示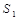 和
和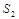 .
.
(2)当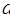 为定值,
为定值,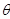 变化时,求“规划合理度”取得最小值时的角
变化时,求“规划合理度”取得最小值时的角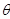 的大小.
的大小.