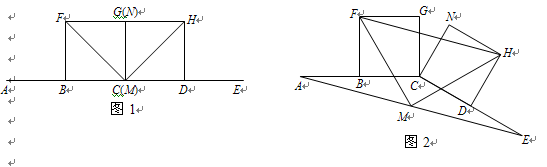如图,在△ABC中,∠ABC,∠ACB的平分线夹角为α,∠ABC的外角平分线与∠ACB的外角平分线的夹角为β,
(1)若α=110°,则∠A= .
(2) 若∠A=30°,则β= .
(3)猜想并证明α与β之间的关系。
已知直角梯形纸片OABC在平面直角坐标系中的位置如图所示,四个顶点的坐标分别为O(0,0),A(10,0),B(8, ),C(0,
),C(0, ),点T在线段OA上(不与线段端点重合),将纸片沿过T点的直线折叠,使点A落在射线AB上(记为点A′),折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;
),点T在线段OA上(不与线段端点重合),将纸片沿过T点的直线折叠,使点A落在射线AB上(记为点A′),折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;
(1)直接写出∠OAB的度数;
(2)当纸片重叠部分的图形是四边形时,直接写出t的取值范围;
(3)求S关于t的解析式及S的最大值.
如图,⊙O的弦AB∥CD,直径BE平分AD于点G,交弦CD于点H,过点B作BF∥AD交CD延长线于点F.
(1)求证:BF与⊙O相切;
(2)求证:DF=DH;
(3)若弦AB=5㎝,AD=8㎝,求⊙O的半径.
学习与探究
(1)请在图1的正方形 内,作出使
内,作出使 的所有点
的所有点 ,并简要说明作法.
,并简要说明作法.
我们可以这样解决问题:利用直径所对的圆周角等于90°,作以AB为直径的圆,则正方形ABCD内部的半圆上所有点(A、B除外)为所求.
(2)请在图2的正方形 内(含边),画出使
内(含边),画出使 的所有的点
的所有的点 ,尺规作图,不写作法,保留痕迹;
,尺规作图,不写作法,保留痕迹;
(3)如图3,已知矩形ABCD中,AB=4,BC=3,请在矩形内(含边),画出 的所有的点
的所有的点 ,尺规作图,不写作法,保留痕迹.
,尺规作图,不写作法,保留痕迹.
已知二次函数y=x2-(2a+3)x+4a+2与x轴交于A、B两点,与y轴交于点C,并且点A在点B左侧,位于原点两侧. 若S△ABC的面积为3,求a的值.
在图1、图2中,线段AC=CE,点B是线段AC的中点,点D是线段CE的中点.四边形BCGF和CDHN都是正方形.AE的中点是M.
如图1,点E在AC的延长线上,点N与点G重合时,点M与点C重合,容易证明FM = MH,FM⊥HM;现将图1中的CE绕点C顺时针旋转一个锐角,得到图2,判断△FMH的形状,并证明你的结论.