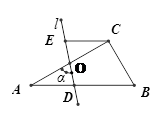
在Rt△ABC中,∠ACB=90°,∠B=60°,BC=4,点O是AC的中点,过点O的直线l从与AC重合的位置开始,绕点O作逆时针旋转,交AB边于点D,过点C作CE∥AB交直线l于E,设直线l的旋转角为α.
当α= 时,四边形EDBC是等腰梯形,此时AD= ;
当α= 时,四边形EDBC是直角梯形,此时AD= ;
试判断EDBC能否为菱形,若能,写出此时α的大小,并证明;若不能,请说明理由.
李红在学校的研究性学习小组中负责了解初一年级200名女生掷实心球的测试成绩.她从中随机调查了若干名女生的测试成绩(单位:米),并将统计结果绘制成了如下的统计图表(内容不完整).
请你结合图表中所提供的信息,回答下列问题:
(1)表中m=________,n=______;
(2)请补全频数分布直方图;
(3)在扇形统计图中,6≤x<7这一组所占圆心角的度数为____________度;
(4)如果掷实心球的成绩达到6米或6米以上为优秀,请你估计该校初一年级女生掷实心球的成绩达到优秀的总人数.
如图, 已知A(-4,-1),B(-5,-4),C(-1,-3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)。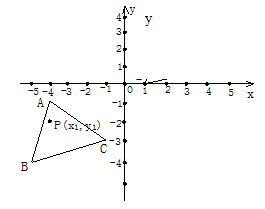
(1)请在图中作出△A′B′C′;
(2)写出点A′、B′、C′的坐标.
已知关于x、y的方程组满足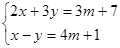 且它的解是一对正数
且它的解是一对正数
(1)试用m表示方程组的解;(2)求m的取值范围;
(3)化简 。
。
解方程组或不等式组
(1)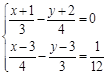 (2)
(2)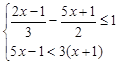
如图,某化工厂与A,B两地有公路和铁路相连,这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5元/(吨•千米),铁路运价为1.2元/(吨•千米),这两次运输共支出公路运费15 000元,铁路运费97 200元,请计算这批产品的销售款比原料费和运输费的和多多少元?
(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:
甲:
乙:
根据甲,乙两名同学所列方程组,请你分别指出未知数x,y表示的意义,然后在等式右边的方框内补全甲、乙两名同学所列方程组.
甲:x表示 ,y表示
乙:x表示 ,y表示
(2)甲同学根据他所列方程组解得x=300,请你帮他解出y的值,并解决该实际问题.