有一种测量压力的电子秤,其原理图如图所示。E是内阻不计、电动势为6V的电源。R0是一个阻值为400Ω的限流电阻。G是由理想电流表改装成的指针式测力显示器。R是一个压敏电阻,其阻值可随压力大小变化而改变,其关系如下表所示。C是一个用来保护显示器的电容器。秤台的重力忽略不计。试分析:
| 压力F/N |
0 |
50 |
100 |
150 |
200 |
250 |
300 |
| 电阻R/Ω |
300 |
280 |
260 |
240 |
220 |
200 |
180 |
(1)利用表中的数据归纳出电阻R随压力F变化的函数式
(2)若电容器的耐压值为5V,该电子秤的最大称量值为多少牛顿?
(3)通过寻求压力与电流表中电流的关系,说明该测力显示器的刻度是否均匀?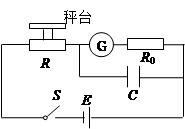
如图所示,厚度为d的玻璃砖与水平实验桌面成45°角放置。红色激光束平行于水平桌面射到玻璃砖的表面,在桌面上得到两个光点A、B,已知玻璃砖对该红色激光的折射率为 。求:AB间的距离L。
。求:AB间的距离L。
如图所示,用销钉固定的导热活塞把水平放置的导热气缸分隔成容积相等的两部分,分别封闭着A、B两部分理想气体。A部分气体压强为pA0=2.5×105Pa,B部分气体压强为pB0=1.5×105Pa。现拔去销钉,待活塞重新稳定后,(外界温度保持不变,活塞与气缸间摩擦可忽略不计,整个过程无漏气发生)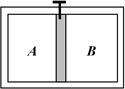
①求此时A部分气体体积与原来体积之比;
②判断此过程中A部分气体是吸热还是放热,并简述理由。
空间三维直角坐标系o-xyz如图所示(重力沿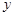 轴负方向),同时存在与xoy平面平行的匀强电场和匀强磁场,它们的方向与x轴正方向的夹角均为
轴负方向),同时存在与xoy平面平行的匀强电场和匀强磁场,它们的方向与x轴正方向的夹角均为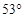 。(已知重力加速度为g,sin53°=0.8,cos53°=0.6)
。(已知重力加速度为g,sin53°=0.8,cos53°=0.6)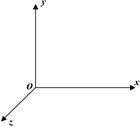
(1)若一电荷量为+q、质量为m的带电质点沿平行于z轴正方向的速度v0做匀速直线运动,求电场强度E和磁感应强度B的大小;
(2)若一电荷量为 、质量为m的带电质点沿平行于z轴正方向以速度v0通过y轴上的点P(0,h,0)时,调整电场使其方向沿x轴负方向、大小为E0。适当调整磁场,则能使带电质点通过坐标Q(h,0,0.5h)点,问通过Q点时其速度大小;
、质量为m的带电质点沿平行于z轴正方向以速度v0通过y轴上的点P(0,h,0)时,调整电场使其方向沿x轴负方向、大小为E0。适当调整磁场,则能使带电质点通过坐标Q(h,0,0.5h)点,问通过Q点时其速度大小;
(3)若一电荷量为 、质量为m的带电质点沿平行于z轴正方向以速度v0通过y轴上的点P(0,0.6h,0)时,改变电场强度大小和方向,同时改变磁感应强度的大小,但不改变其方向,带电质点做匀速圆周运动能经过x轴上的某点M,问电场强度
、质量为m的带电质点沿平行于z轴正方向以速度v0通过y轴上的点P(0,0.6h,0)时,改变电场强度大小和方向,同时改变磁感应强度的大小,但不改变其方向,带电质点做匀速圆周运动能经过x轴上的某点M,问电场强度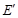 和磁感应强度
和磁感应强度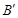 的大小满足什么条件?并求出带电质点经过x轴M点的时间。
的大小满足什么条件?并求出带电质点经过x轴M点的时间。
某一长直的赛道上,有一辆F1赛车前方200m处有一安全车正以10m/s的速度匀速前进,这时赛车从静止出发以2m/s2的加速度追赶。求:
(1)赛车出发经多长时间追上安全车。
(2)当赛车刚追上安全车时,赛车手立即刹车,使赛车以4m/s2的加速度做匀减速直线运动,再经过多长时间两车第二次相遇。
交通规则规定:绿灯时通行的汽车,红灯亮起时,车头已越过停车线的汽车允许通过。如右图所示,停止线AB与前方斑马线边界CD间的距离为23m。车长7m的卡车以54km/h的速度向北匀速行驶。
(1)晚十一点凌晨四点,该信号灯被改为持续闪烁的黄灯,并设置AB、CD路段间限速18km/h。司机停止线AB前80m处发现黄灯,立即开始减速。车头刚好到达AB处速度恰好为18km/h,并以该速度匀速通过此路段。当车尾经过CD线时,卡车开始做a1=4m/s2的匀加速运动,直至恢复原来的速度。求司机因为黄灯而耽误的时间?
(2)早晚高峰期间,该处恢复红绿信号灯。红灯时,AB停止线拦下很多汽车,拦停的汽车笔直地排成一排。相邻两车车头相距L=8m,当绿灯显示“30”时,第一辆汽车启动并做a2=3m/s2的匀加速直线运动,加速到54km/h后匀速运动。事实上,第一个司机看见绿灯到启动需要反应时间0.6s,后一辆车看见前一辆车启动后同样需要反应时间0.6s,问绿灯结束后多少辆汽车通过停止线?