如图所示,在半径为a的圆形区域内充满磁感应强度大小为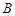 的均匀磁场,其方向垂直于纸面向里.在圆形区域平面内固定放置一绝缘材料制成的边长为L=1.2a的刚性等边三角形框架
的均匀磁场,其方向垂直于纸面向里.在圆形区域平面内固定放置一绝缘材料制成的边长为L=1.2a的刚性等边三角形框架 ,其中心
,其中心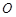 位于圆形区域的圆心.
位于圆形区域的圆心.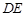 边上
边上 点(DS=L/2)处有一发射带电粒子源,发射粒子的方向皆在图示平面内且垂直于
点(DS=L/2)处有一发射带电粒子源,发射粒子的方向皆在图示平面内且垂直于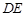 边,发射粒子的电量皆为
边,发射粒子的电量皆为 (>0),质量皆为
(>0),质量皆为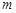 ,但速度
,但速度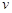 有各种不同的数值.若这些粒子与三角形框架的碰撞均无机械能损失,并要求每一次碰撞时速度方向垂直于被碰的边.试问:(1)若发射的粒子速度垂直于
有各种不同的数值.若这些粒子与三角形框架的碰撞均无机械能损失,并要求每一次碰撞时速度方向垂直于被碰的边.试问:(1)若发射的粒子速度垂直于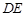 边向上,这些粒子中回到
边向上,这些粒子中回到 点所用的最短时间是多少?(2)若发射的粒子速度垂直于
点所用的最短时间是多少?(2)若发射的粒子速度垂直于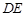 边向下,带电粒子速度
边向下,带电粒子速度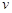 的大小取哪些数值时可使
的大小取哪些数值时可使 点发出的粒子最终又回到
点发出的粒子最终又回到 点?这些粒子中,回到
点?这些粒子中,回到 点所用的最短时间是多少?(不计粒子的重力和粒子间的相互作用)
点所用的最短时间是多少?(不计粒子的重力和粒子间的相互作用)
如图所示,质量为km的斜劈,其中k>1,静止放在光滑的水平面上,斜劈的曲面光滑且为半径为R的四分之一圆面,圆面下端与光滑水平面相切。一质量为m的小球位于水平面上某位置,现给小球水平向右的初速度v0。
①若R足够大,求当小球从斜劈滑下离开时小球的速度 ;
;
②若小球向右滑上斜劈刚好没有越过圆面上端,求k的取值 .
用折射率为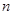 的透明物质做成内、外径分别为
的透明物质做成内、外径分别为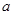 、
、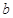 的球壳,球壳的内表面涂有能完全吸收光的物质,如图所示,当一束平行光从左侧射向该球壳时,被吸收掉的光束在射进球壳左侧外表面前的横截面积有多大?
的球壳,球壳的内表面涂有能完全吸收光的物质,如图所示,当一束平行光从左侧射向该球壳时,被吸收掉的光束在射进球壳左侧外表面前的横截面积有多大?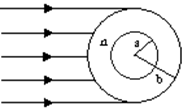
用质子流(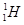 )轰击固态的重水
)轰击固态的重水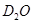 ,当质子和重水中的氘核(
,当质子和重水中的氘核(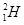 )发生碰撞时,系统损失的动能如果达到核反应所需的能量,将发生生成
)发生碰撞时,系统损失的动能如果达到核反应所需的能量,将发生生成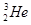 核的反应。
核的反应。
①写出质子流轰击固态的重水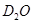 的核反应方程;
的核反应方程;
②当质子具有最小动能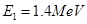 时,用质子流轰击固态的重水
时,用质子流轰击固态的重水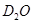 (认为氘核是静止的)可发生核反应;若用氘核轰击普通水的固态冰中的质子(认为质子是静止的)时,也能发生同样的核反应,求氘核的最小动能
(认为氘核是静止的)可发生核反应;若用氘核轰击普通水的固态冰中的质子(认为质子是静止的)时,也能发生同样的核反应,求氘核的最小动能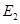 。已知氘核质量等于质子质量的两倍。
。已知氘核质量等于质子质量的两倍。
如图所示,一束截面为圆形(半径R)的平行白光垂直射向一玻璃半球的平面,经折射后在屏幕S上形成一个圆形彩色亮区。已知玻璃半球的半径为R,屏幕S至球心的距离为d(d>3R),不考虑光的干涉和衍射,试问: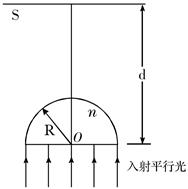
①在屏幕S上形成的圆形亮区的最外侧是什么颜色?
②若玻璃半球对最外侧色光的折射率为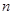 ,求出圆形亮区的最大半径。
,求出圆形亮区的最大半径。
如图所示,足够长的圆柱形气缸竖直放置,其横截面积为S=1×10-3m2,气缸内有质量m=2kg的活塞,活塞与气缸壁封闭良好,不计摩擦。开始时活塞被销子K销于如图位置,离缸底L1=12cm,此时气缸内被封闭气体的压强为P1=1.5×105 Pa,温度为T1=300K。外界大气压为P0=1.0×105Pa,g=10m/s2。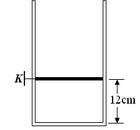
①现对密闭气体加热,当温度升到T2=400K,其压强P2多大?
②若在此时拔去销子K,活塞开始向上运动,当它最后静止在某一位置时,气缸内气体的温度降为T3=360K,则这时活塞离缸底的距离L3为多少?
③保持气体温度为360K不变,让气缸和活塞一起在竖直方向作匀变速直线运动,为使活塞能停留在离缸底L4=16cm处,则求气缸和活塞应作匀加速直线运动的加速度a大小及方向。