已知某种水果的批发单价与批发量的函数关系如图（1）所示．请说明图中①、②两段函数图象的实际意义．
写出批发该种水果的资金金额w（元）与批发量m（kg）之间的函数关系式；在下图的坐标系中画出该函数图象；指出金额在什么范围内，以同样的资金可以批发到较多数量的该种水果
经调查，某经销商销售该种水果的日最高销量与零售价之间的函数关系如图（2）所示，该经销商拟每日售出60kg以上该种水果，且当日零售价不变，请你帮助该经销商设计进货和销售的方案，使得当日获得的利润最大．
超速行驶是引发交通事故的主要原因．上周末，小明和三位同学尝试用自己所学的知识检测车速，如图，观测点设在到县城城南大道的距离为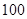
米的点P处．这时，一辆出租车由西向东匀速行驶，测得此车从A处行驶到B处所用的时间为
秒且∠APO=60°，∠BPO =45°． 
求A、B之间的路程
请判断此出租车是否超过了城南大道每小时60千米的限制速度？
（参考数据：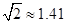
，
）
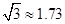如图，已知
的三个顶点的坐标分别为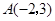
、
、
．
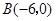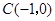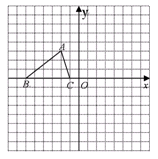
请直接写出点
关于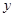
轴对称的点的坐标将
绕坐标原点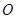
逆时针旋转90°．画出图形，直接写出点
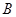的对应点的坐标请直接写出：以
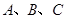为顶点的平行四边形的第四个顶点
的坐标．
计算：计算： 2
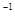－tan60°+(
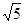－1)
解方程：
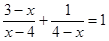
如图，平面直角坐标系中，四边形OABC为菱形，点A在x轴的正半轴上，BC与y轴交于点D，点C的坐标为（-3，4）。点A的坐标为▲；
求过点A、O、C的抛物线解析式，并求它的顶点坐标；
在直线AB上是否存在点P，使得以点A、O、P为顶点的三角形与△COD相似。若存在，求出点P的坐标；若不存在，请说明理由。
阅读理解：通过学习三角函数，我们知道在直角三角形中，一个锐角的大小，与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化。类似地，可以在等腰三角形中，建立边角之间的联系。我们定义：等腰三角形中底边长与腰长的比叫做顶角正对（sad）。如图1，在⊿ABC中，AB=AC，顶角A的正对记作sadA，这时sadA=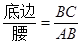
。容易知道一个角的大小，与这个角的正对值也是相互唯一确定的。根据上述角的正对定义，解下列问题：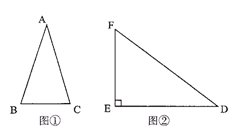
计算：sad60°=▲
对于0°＜A＜90°，∠A的正对值sadA的取值范围是▲；
如图2，已知△DEF中，∠E=90°，cosD=
，试求sadD的值。