阅读理解：通过学习三角函数，我们知道在直角三角形中，一个锐角-优题课

阅读理解：通过学习三角函数，我们知道在直角三角形中，一个锐角的大小，与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化。类似地，可以在等腰三角形中，建立边角之间的联系。我们定义：等腰三角形中底边长与腰长的比叫做顶角正对（sad）。如图1，在⊿ABC中，AB=AC，顶角A的正对记作sadA，这时sadA=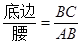。容易知道一个角的大小，与这个角的正对值也是相互唯一确定的。根据上述角的正对定义，解下列问题：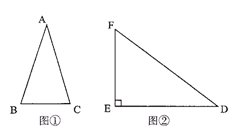

计算：sad60°= ▲
对于0°＜A＜90°，∠A的正对值sadA的取值范围是 ▲ ；
如图2，已知△DEF中，∠E=90°，cosD=，试求sadD的值。

科目数学题型解答题难度中等

知识点：三角形的五心

已知反比例函数 $y_{1} = \frac{k}{x}$ 的图象与一次函数 $y_{2} = ax + b$ 的图象交于点 $A (1, 4)$ 和点 $B (m, - 2)$ ．

（1）求这两个函数的表达式；

（2）根据图象直接写出一次函数的值大于反比例函数的值的 $x$ 的取值范围．

如图， $DB / / AC$ ，且 $DB = \frac{1}{2} AC$ ， $E$ 是 $AC$ 的中点，

（1）求证： $BC = DE$ ；

（2）连接 $AD$ 、 $BE$ ，若要使四边形 $DBEA$ 是矩形，则需给 $ΔABC$ 添加什么条件，为什么？

如图，在平面直角坐标系中， $Rt Δ ABC$ 的三个顶点分别是 $A (- 8, 3)$ ， $B (- 4, 0)$ ， $C (- 4, 3)$ ， $∠ ABC = α °$ ．抛物线 $y = \frac{1}{2} x^{2} + bx + c$ 经过点 $C$ ，且对称轴为 $x = - \frac{4}{5}$ ，并与 $y$ 轴交于点 $G$ ．

（1）求抛物线的解析式及点 $G$ 的坐标；

（2）将 $Rt Δ ABC$ 沿 $x$ 轴向右平移 $m$ 个单位，使 $B$ 点移到点 $E$ ，然后将三角形绕点 $E$ 顺时针旋转 $α °$ 得到 $ΔDEF$ ．若点 $F$ 恰好落在抛物线上．

①求 $m$ 的值；

②连接 $CG$ 交 $x$ 轴于点 $H$ ，连接 $FG$ ，过 $B$ 作 $BP / / FG$ ，交 $CG$ 于点 $P$ ，求证： $PH = GH$ ．

如图， $ΔABC$ 中， $∠ BAC = 120 °$ ， $AB = AC = 6$ ． $P$ 是底边 $BC$ 上的一个动点 $(P$ 与 $B$ 、 $C$ 不重合），以 $P$ 为圆心， $PB$ 为半径的 $⊙ P$ 与射线 $BA$ 交于点 $D$ ，射线 $PD$ 交射线 $CA$ 于点 $E$ ．

（1）若点 $E$ 在线段 $CA$ 的延长线上，设 $BP = x$ ， $AE = y$ ，求 $y$ 关于 $x$ 的函数关系式，并写出 $x$ 的取值范围．

（2）当 $BP = 2 \sqrt{3}$ 时，试说明射线 $CA$ 与 $⊙ P$ 是否相切．

（3）连接 $PA$ ，若 $S_{ΔAPE} = \frac{1}{8} S_{ΔABC}$ ，求 $BP$ 的长．

上网流量、语音通话是手机通信消费的两大主体，目前，某通信公司推出消费优惠新招 $- -$ “定制套餐”，消费者可根据实际情况自由定制每月上网流量与语音通话时间，并按照二者的阶梯资费标准缴纳通信费．下表是流量与语音的阶梯定价标准．

流量阶梯定价标准
使用范围	阶梯单价（元 $/ MB)$
$1 - 100 MB$	$a$
$101 - 500 MB$	0.07
$501 MB - 20 GB$	$b$

语音阶梯定价标准
使用范围	阶梯资费（元 $/$ 分钟）
$1 - 500$ 分钟	0.15
$501 - 1000$ 分钟	0.12
$1001 - 2000$ 分钟	$m$

【小提示：阶梯定价收费计算方法，如600分钟语音通话费 = 0 . 15 × 500 + 0 . 12 × ( 600 − 500 ) = 87 元】

（1）甲定制了 $600 MB$ 的月流量，花费48元；乙定制了 $2 GB$ 的月流量，花费120.4元，求 $a$ ， $b$ 的值．（注 $: 1 GB = 1024 MB)$

（2）甲的套餐费用为199元，其中含 $600 MB$ 的月流量；丙的套餐费用为244.2元，其中包含 $1 GB$ 的月流量，二人均定制了超过1000分钟的每月通话时间，并且丙的语音通话时间比甲多300分钟，求 $m$ 的值．