如图，某农户想利用自家院子一面墙和20米长的篱笆围成一个矩形养鸡场，并留出一个1米宽的口子用来进出．若围成的养鸡场面积为
，求围成的养鸡场的长和宽；请用配方法，求出能围成的矩形养鸡场的最大面积，并说明设计方案．
二次函数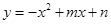
的图象经过点A（﹣1，4），B（1，0），
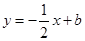经过点B，且与二次函数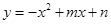交于点D．过点D作DC⊥x轴，垂足为点C．
（1）求二次函数的表达式；
（2）点N是二次函数图象上一点（点N在BD上方），过N作NP⊥x轴，垂足为点P，交BD于点M，求MN的最大值．
给出如下规定：两个图形G1和G2，点P为G1上任一点，点Q为G2上任一点，如果线段PQ的长度存在最小值，就称该最小值为两个图形G1和G2之间的距离．在平面直角坐标系xOy中，O为坐标原点．
（1）点A的坐标为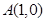
，则点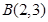
和射线OA之间的距离为________，点
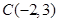和射线OA之间的距离为________；
（2）如果直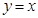线
和双曲线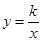
之间的距离为
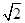，那么k=；（可在图1中进行研究）
（3）点E的坐标为（1，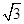
），将射线OE绕原点O逆时针旋转60°，得到射线OF，在坐标平面内所有和射线OE，OF之间的距离相等的点所组成的图形记为图形M．
①请在图2中画出图形M，并描述图形M的组成部分；（若涉及平面中某个区域时可以用阴影表示）
②将射线OE，OF组成的图形记为图形W，抛物线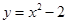
与图形M的公共部分记为图形N，请直接写出图形W和图形N之间的距离．
△ABC中，AB=AC．取BC边的中点D，作DE⊥AC于点E，取DE的中点F，连接BE，AF交于点H．
（1）如图1，如果
，那么
°，
；
（2）如图2，如果
，猜想
的度数和
的值，并证明你的结论；
（3）如果
，那么．（用含
的表达式表示）
已知二次函数
的图象
经过
，
两点．
（1）求对应的函数表达式；
（2）将先向左平移1个单位，再向上平移4个单位，得到抛物线
，将对应的函数表达式记为
，求对应的函数表达式；
（3）设
，在（2）的条件下，如果在
≤x≤a内存在某一个x的值，使得
≤
成立，利用函数图象直接写出a的取值范围．
阅读下面的材料：
小敏在数学课外小组活动中遇到这样一个问题：
如果α，β都为锐角，且
，
，求
的度数．
小敏是这样解决问题的：如图1，把
，
放在正方形网格中，使得
，
，且BA，BC在直线BD的两侧，连接AC，可证得△ABC是等腰直角三角形，因此可求得
="∠ABC" =
°．
请参考小敏思考问题的方法解决问题：
如果，都为锐角，当
，
时，在图2的正方形网格中，利用已作出的锐角α，画出∠MON=
，由此可得=______°．