设函数 。
。
(1)求函数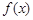 的极大值;
的极大值;
(2)若 时,恒有
时,恒有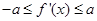 成立(其中
成立(其中 是函数
是函数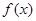 的导函数),试确定实数
的导函数),试确定实数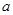 的取值范围。
的取值范围。
(本小题满分8分)设等差数列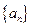 的前
的前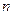 项和为
项和为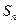 , 已知
, 已知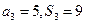 .
.
(Ⅰ)求首项 和公差
和公差 的值;(Ⅱ)若
的值;(Ⅱ)若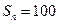 ,求
,求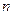 的值.
的值.
(本小题满分8分)试证明函数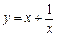 在
在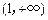 上为增函数.
上为增函数.
(本小题满分14分)设椭圆 (a>b>0)的左焦点为F1(-2,0),左准线 L1 与x轴交于点N(-3,0),过点N且倾斜角为300的直线L交椭圆于A、B两点。
(a>b>0)的左焦点为F1(-2,0),左准线 L1 与x轴交于点N(-3,0),过点N且倾斜角为300的直线L交椭圆于A、B两点。
(1)求直线L和椭圆的方程;
(2)求证:点F1(-2,0)在以线段AB为直径的圆上
(本小题满分12分)求经过点P(―3,2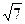 )和Q(―6
)和Q(―6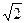 ,―7)且焦点在坐标轴上的双曲线的标准方程。
,―7)且焦点在坐标轴上的双曲线的标准方程。
(本小题满分12分)已知p:x < -2,或x > 10;q: ≤x≤
≤x≤ ;若¬p是q的充分而不必要条件,求实数
;若¬p是q的充分而不必要条件,求实数 的取值范围。
的取值范围。