(本小题满分12分)
已知函数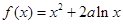 .
.
(1)若函数 的图象在
的图象在 处的切线斜率为
处的切线斜率为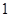 ,求实数
,求实数 的值;
的值;
(2)在(1)的条件下,求函数 的单调区间;
的单调区间;
(3)若函数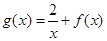 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围.
的取值范围.
已知 ,求
,求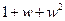 的值。
的值。
已知 ,其中x,y∈R,求x,y。
,其中x,y∈R,求x,y。
(本题满分10分)选修4-1:几何证明选讲
如图,圆O的直径AB=10,弦DE⊥AB于点H,
AH=2.
(Ⅰ)求DE的长;
(Ⅱ)延长ED到P,过P作圆O的切线,切点为C,
若PC=2 ,求PD的长.
,求PD的长.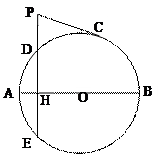
.(本题满分12分)
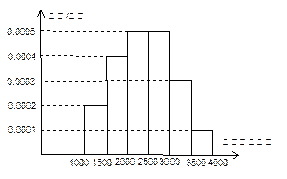 |
某地统计局就本地居民的月收入调查了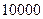 人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组
人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组
表示收入在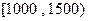 之间).
之间).
(Ⅰ)根据频率分布直方图估计样本
数据的中位数所在的区间;
(Ⅱ)求被调查居民月收入在 之间的人数;
之间的人数;
(Ⅲ)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这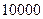 人中,用分层抽样方法抽出
人中,用分层抽样方法抽出 人作进一步分析,则月收入在
人作进一步分析,则月收入在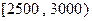 的这段应抽多少人?
的这段应抽多少人?
(本题满分12分)
在长方体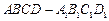 中,
中,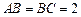 ,过
,过 、
、 、
、 三点的平面截去长方体的一个角后,得到如图所示的几
三点的平面截去长方体的一个角后,得到如图所示的几
何体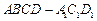 ,且这个几何体的体积为
,且这个几何体的体积为 .
.
(Ⅰ)求棱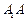 的长;
的长;
(Ⅱ)若 的中点为
的中点为 ,求异面直线
,求异面直线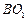 与
与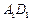 所成角
所成角
的余弦值.