已知函数
为常数,
=2.71828…是自然对数的底数),曲线
在点
处的切线与
轴平行.
(Ⅰ)求
的值;
(Ⅱ)求
的单调区间;
(Ⅲ)设
,其中
为
的导函数.证明:对任意
.
一个多面体的三视图和直观图如图所示,其中 、
、 分别是
分别是 、
、 的中点,
的中点, 是
是 上的一动点。
上的一动点。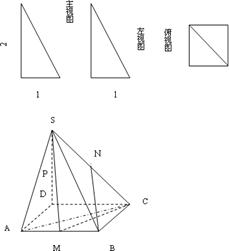
(1)求证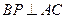 ;
;
(2)当点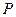 落在什么位置时,
落在什么位置时,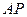 平行于平面
平行于平面 ?
?
(3)求三棱锥 的体积。
的体积。
 中内角
中内角 、
、 、
、 的对边分别为
的对边分别为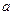 、
、 、
、 ,向量m
,向量m ,n
,n 且m
且m n
n
(1)求锐角 的大小;
的大小;
(2)如果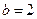 ,求
,求 的面积
的面积 的最大值。
的最大值。
设数列 前
前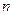 项和为
项和为 ,点
,点
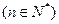 均在函数
均在函数 图象上。
图象上。
(1)求数列 的通
的通 项公式;
项公式;
(2)设 ,
,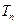 是数列
是数列 的前
的前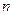 项和,求使得
项和,求使得 对所有
对所有 都成立的最小正整数
都成立的最小正整数 。
。
(本小题满分12分)
椭圆G: 的左、右焦点分别为
的左、右焦点分别为 ,M是椭圆上的一点,且满足
,M是椭圆上的一点,且满足 =0.
=0.
(1)求离心率e的取值范围;
(1)当离心率e取得最小值时,点N(0,3)到椭圆上的点的最远距离为5 .
.
①求此时椭圆G的方程;
②设斜率为 的直线l与椭圆G相交于不同的两点A、B,Q为AB的中点,
的直线l与椭圆G相交于不同的两点A、B,Q为AB的中点,
问:A、B两点能否关于过点 、Q的直线对称?若能,求出k的取值范
、Q的直线对称?若能,求出k的取值范
围;若不能,请说明理由.
(本小题满分12分)
设数列 的前
的前 项和为
项和为 已知
已知

(1)设 ,证明数列
,证明数列 是等比数列;
是等比数列;
(2)求数列 的通项公式;
的通项公式; (3)若
(3)若 ,
, 为
为 的前n项和,求证:
的前n项和,求证:
 .
.