(本小题满分12分)
椭圆G: 的左、右焦点分别为
的左、右焦点分别为 ,M是椭圆上的一点,且满足
,M是椭圆上的一点,且满足 =0.
=0.
(1)求离心率e的取值范围;
(1)当离心率e取得最小值时,点N(0,3)到椭圆上的点的最远距离为5 .
.
①求此时椭圆G的方程;
②设斜率为 的直线l与椭圆G相交于不同的两点A、B,Q为AB的中点,
的直线l与椭圆G相交于不同的两点A、B,Q为AB的中点,
问:A、B两点能否关于过点 、Q的直线对称?若能,求出k的取值范
、Q的直线对称?若能,求出k的取值范
围;若不能,请说明理由.
在锐角△ABC中,cos B+cos (A-C)= sin C.
sin C.
(Ⅰ) 求角A的大小;
(Ⅱ) 当BC=2时,求△ABC面积的最大值.
命题P:函数 内单调递减;命题Q:曲线
内单调递减;命题Q:曲线 轴交于不同的两点.
轴交于不同的两点.
如果“P\/Q”为真且“P/\Q”为假,求a的取值范围.
已知函数

(I)若
 的一个极值点,求a的值;
的一个极值点,求a的值;
(II)求证:当 上是增函数;
上是增函数;
(III)若对任意的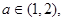 总存在
总存在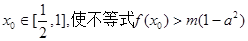 成立,求实数m的取值范围。
成立,求实数m的取值范围。
已知函数 ,实数a,b为常数),
,实数a,b为常数),
(1)若a=1,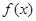 在(0,+∞)上是单调增函数,求b的取值范围;
在(0,+∞)上是单调增函数,求b的取值范围;
(2)若a≥2,b=1,判断方程 在(0,1]上解的个数
在(0,1]上解的个数
已知集合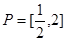 ,函数
,函数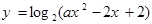 的定义域为
的定义域为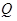 ,
,
(1)若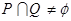 ,求实数
,求实数 的取值范围;
的取值范围;
(2)若方程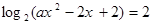 在
在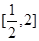 内有解,求实数
内有解,求实数 的取值范围
的取值范围