已知函数 .
.
(1)判断并证明 的奇偶性;
的奇偶性;
(2)求证: ;
;
(3)已知a,b∈(-1,1),且 ,
, ,求
,求 ,
, 的值.
的值.
已知的顶点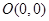 、
、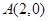 、
、 ,
, 边上的中线所在直线为
边上的中线所在直线为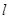 .(1)求
.(1)求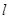 的方程;(2)求点A关于直线
的方程;(2)求点A关于直线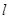 的对称点的坐标。
的对称点的坐标。
已知椭圆的长轴长为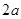 ,焦点是
,焦点是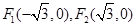 ,点
,点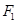 到直线
到直线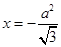 的距离为
的距离为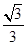 ,过点
,过点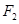 且倾斜角为锐角的直线
且倾斜角为锐角的直线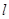 与椭圆交于A、B两点,使得|
与椭圆交于A、B两点,使得|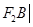 =3|
=3|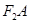
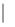 .
.
(1)求椭圆的标准方程;
(2)求直线l的方程.
设函数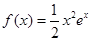 .
.
(1)求f(x)的单调区间;
(2)若当x∈[-2,2]时,不等式f(x)>m恒成立,求实数m的取值范围.
在极坐标系中,已知圆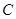 经过点
经过点 ,圆心为直线
,圆心为直线 与极轴的交点,求圆
与极轴的交点,求圆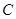 的极坐标方程.
的极坐标方程.
在直角坐标系中,以原点为极点, 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线
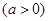 ,过点
,过点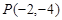 的直线
的直线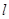 的参数方程为:
的参数方程为:
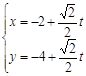 ,(t为参数),直线
,(t为参数),直线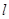 与曲线
与曲线 分别交于
分别交于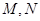 两点.
两点.
(1)写出曲线 和直线
和直线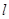 的普通方程;
的普通方程;
(2)若 成等比数列,求
成等比数列,求 的值.
的值.