已知椭圆的长轴长为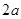 ,焦点是
,焦点是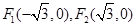 ,点
,点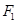 到直线
到直线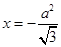 的距离为
的距离为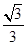 ,过点
,过点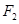 且倾斜角为锐角的直线
且倾斜角为锐角的直线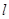 与椭圆交于A、B两点,使得|
与椭圆交于A、B两点,使得|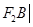 =3|
=3|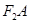
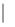 .
.
(1)求椭圆的标准方程;
(2)求直线l的方程.
如图,正方形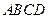 所在平面与圆
所在平面与圆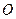 所在平面相交于
所在平面相交于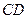 ,线段
,线段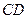 为圆
为圆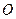 的弦,
的弦,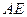 垂直于圆
垂直于圆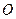 所在平面,垂足
所在平面,垂足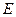 是圆
是圆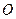 上异于
上异于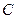 .
.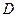 的点,
的点,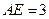 ,圆
,圆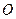 的直径为9.
的直径为9.
(I)求证:平面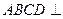 平面
平面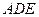 ;
;
(II)求二面角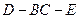 的平面角的正切值.
的平面角的正切值.
象棋比赛中,胜一局得2分,负一局得0分,和棋一局得1分,在甲对乙的每局比赛中,甲胜、和、负的概率依次为0.5,0.3,0.2.现此二人进行两局比赛,得分累加。
(I)求甲得2分的概率;
(II)记甲得分为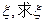 的分布列和期望
的分布列和期望
已知函数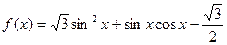
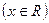 .
.
(Ⅰ)若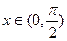 ,求
,求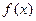 的最大值;
的最大值;
(Ⅱ)在 中,若
中,若 ,
,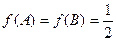 ,求
,求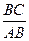 的值
的值
(本小题14分)
已知函 数
数
 .
.
(Ⅰ)若 ,求曲线
,求曲线 在
在 处切线的斜率;
处切线的斜率;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)设 ,若对任意
,若对任意 ,均存在
,均存在 ,使得
,使得 ,求
,求 的取值范围。
的取值范围。
((本小题12分)已知函数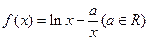 。
。
(1)判断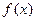 在定义域上的单调性;
在定义域上的单调性;
(2)若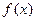 在
在 上的最小值为2,求
上的最小值为2,求 的值。
的值。