(本题12分)对于函数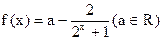 为奇函数(Ⅰ)求
为奇函数(Ⅰ)求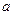 的值;(Ⅱ)用函数单调性定义及指数函数性质证明:
的值;(Ⅱ)用函数单调性定义及指数函数性质证明:  在
在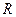 上是增函数。
上是增函数。
设函数
的所有正的极小值点从小到大排成的数列为
.
(Ⅰ)求数列
的通项公式.
(Ⅱ)设
的前
项和为
,求
.
如图, 分别是椭圆 : 的左、右焦点, 是椭圆 的顶点, 是直线 与椭圆 的另一个交点, .
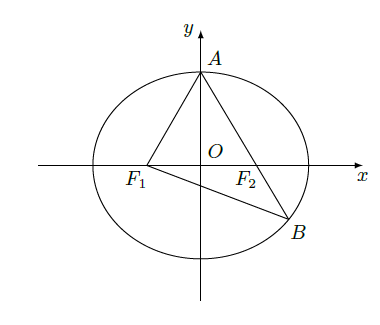
(Ⅰ)求椭圆
的离心率;
(Ⅱ)已知
的面积为
,求
的值.
如图,长方体 中,底面 是正方形, 是 的中点, 是棱 上任意一点.
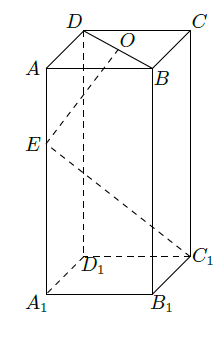
(Ⅰ)证明:
;
(Ⅱ)如果
=
,
=
,
, 求
的长.
若某产品的直径长与标准值的差的绝对值不超过
时,则视为合格品,否则视为不合格品。在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取
件进行检测,结果发现有
件不合格品。计算这
件不合格品的直径长与标准值的差(单位:
), 将所得数据分组,得到如下频率分布表:
| 分组 |
频数 |
频率 |
| [-3, -2) |
0.10 |
|
| [-2, -1) |
8 |
|
| (1,2] |
0.50 |
|
| (2,3] |
10 |
|
| (3,4] |
||
| 合计 |
50 |
1.00 |
(Ⅰ)将上面表格中缺少的数据填在相应位置;
(Ⅱ)估计该厂生产的此种产品中,不合格品的直径长与标准值的差落在区间(1,3]内的概率;
(Ⅲ)现对该厂这种产品的某个批次进行检查,结果发现有20件不合格品。据此估算这批产品中的合格品的件数。
设定义在( )上的函数
(Ⅰ)求
的最小值;
(Ⅱ)若曲线
在点
处的切线方程为
,求
的值。