(本小题满分l2分)某市第一中学要用鲜花布置花圃中 五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.
五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.
(1)当 区域同时用红色鲜花时,求布置花圃的不同方法的种数;
区域同时用红色鲜花时,求布置花圃的不同方法的种数;
(2)求恰有两个区域用红色鲜花的概率;
(3)记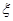 为花圃中用红色鲜花布置的区域的个数,求随机变量
为花圃中用红色鲜花布置的区域的个数,求随机变量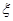 的分布列及其数学期望.
的分布列及其数学期望.
如图,直三棱柱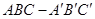 的侧棱长为3,
的侧棱长为3,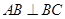 ,且
,且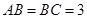 ,
,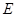 、
、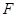 分别是棱
分别是棱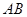 、
、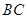 上的动点,且
上的动点,且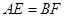
(1)证明:无论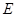 在何处,总有
在何处,总有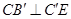 ;
;
(2)当三棱柱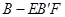 .的体积取得最大值时,求异面直线
.的体积取得最大值时,求异面直线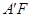 与
与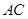 所成角的余弦值.
所成角的余弦值.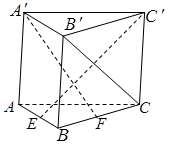
已知向量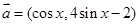 ,
, ,
,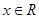 ,设函数
,设函数 .
.
(1)求函数 的最大值;
的最大值;
(2)在 中,角
中,角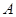 为锐角,角
为锐角,角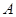 、
、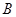 、
、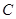 的对边分别为
的对边分别为 、
、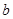 、
、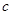 ,
,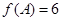 ,且
,且 的面积为3,
的面积为3,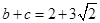 ,求
,求 的值.
的值.
已知函数 ,且
,且 在
在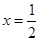 处的切线方程为
处的切线方程为 .
.
(1)求 的解析式;
的解析式;
(2)证明:当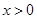 时,恒有
时,恒有 ;
;
(3)证明:若 ,
, ,且
,且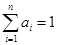 ,则
,则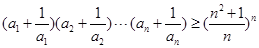 .
.
已知椭圆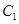 ,抛物线
,抛物线 的焦点均在
的焦点均在 轴上,
轴上,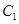 的中心和
的中心和 的顶点均为原点
的顶点均为原点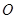 ,每条曲线上取两个点,将其坐标记录于表中:
,每条曲线上取两个点,将其坐标记录于表中:
 |
 |
 |
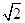 |
 |
 |
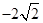 |
 |
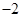 |
 |
(1)求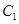 ,
, 的标准方程;
的标准方程;
(2)设斜率不为0的动直线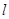 与
与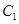 有且只有一个公共点
有且只有一个公共点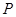 ,且与
,且与 的准线交于
的准线交于 ,试探究:在坐标平面内是否存在定点
,试探究:在坐标平面内是否存在定点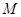 ,使得以
,使得以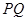 为直径的圆恒过点
为直径的圆恒过点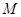 ?若存在,求出
?若存在,求出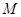 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
已知数列 中,
中, ,
,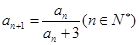 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若数列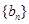 满足
满足 ,数列
,数列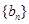 的前
的前 项和为
项和为 ,若不等式
,若不等式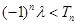 对一切
对一切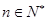 恒成立,求
恒成立,求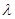 的取值范围.
的取值范围.