如图，矩形ABCD中，AB=4，AD=5，将矩形ABCD绕点A顺时针旋转，得到矩形AMNP，直线MN分别与边BC、CD交于点E、F.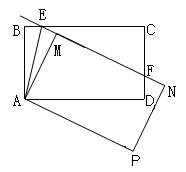
判断BE与ME的数量关系，并加以证明；
当△CEF是等腰三角形时，求线段BE的长；
设x=BE，y=CF·（AB2-BE2），试求y与x之间的函数关系式，并求出y的最大值.
某商场第一次用11000元购进某款拼装机器人进行销售，很快销售一空，商家又用24000元第二次购进同款机器人，所购进数量是第一次的2倍，但单价贵了10元．
（1）求该商家第一次购进机器人多少个？
（2）若所有机器人都按相同的标价销售，要求全部销售完毕的利润率不低于20%（不考虑其它因素），那么每个机器人的标价至少是多少元？
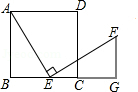
如图，在正方形ABCD中，点E（与点B、C不重合）是BC边上一点，将线段EA绕点E顺时针旋转90°到EF，过点F作BC的垂线交BC的延长线于点G，连接CF．
（1）求证：△ABE≌△EGF；
（2）若AB＝2，S△ABE＝2S△ECF，求BE．
已知反比例函数 与一次函数y＝x+2的图象交于点A（﹣3，m）
（1）求反比例函数的解析式；
（2）如果点M的横、纵坐标都是不大于3的正整数，求点M在反比例函数图象上的概率．
甲、乙两名射击运动员在某次训练中各射击10发子弹，成绩如表：
|
甲 |
8 |
9 |
7 |
9 |
8 |
6 |
7 |
8 |
10 |
8 |
|
乙 |
6 |
7 |
9 |
7 |
9 |
10 |
8 |
7 |
7 |
10 |
且
＝8，S乙2＝1.8，根据上述信息完成下列问题：
（1）将甲运动员的折线统计图补充完整；
（2）乙运动员射击训练成绩的众数是 ，中位数是 ．
（3）求甲运动员射击成绩的平均数和方差，并判断甲、乙两人本次射击成绩的稳定性．
如图，矩形的边OA在x轴上，边OC在y轴上，点B的坐标为（10，8），沿直线OD折叠矩形，使点A正好落在BC上的E处，E点坐标为（6，8），抛物线y＝ax2+bx+c经过O、A、E三点．
（1）求此抛物线的解析式；
（2）求AD的长；
（3）点P是抛物线对称轴上的一动点，当△PAD的周长最小时，求点P的坐标．
