如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,E点坐标为(6,8),抛物线y=ax2+bx+c经过O、A、E三点.
(1)求此抛物线的解析式;
(2)求AD的长;
(3)点P是抛物线对称轴上的一动点,当△PAD的周长最小时,求点P的坐标.

(本小题满分10分)如图,⊙O是△ABC的外接圆,AB=AC=10,BC=12,P是圆上的一个动点,过点P作BC的平行线交AB的延长线于点D.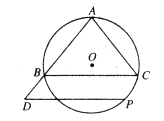
(1)当点P在什么位置时,DP是⊙O的切线?请说明理由;
(2)当DP为⊙O的切线时,求线段DP的长.
(本小题满分10分)某商店第一次用600元购进某种铅笔若干支,第二次又用600元购进该种铅笔,但这次每支的进价比第一次贵l元,所以购进数量比第一次少了30支.
(1)求第一次每支铅笔的进价及购进的数量;
(2)若将这两次购进的铅笔按同一单价x(元,支)全部销售完毕,并要求获利不低于420元,求获利y(元)关于单价x(元/支)的函数关系式及定义域,并在直角坐标系内画出它的大致图象.
(本小题满分10分)已知:如图,在直角梯形ABCD中,AD∥BC,AB⊥AD,BC=CD,BE⊥CD,垂足为点E,点F在BD上,连接AF,EF.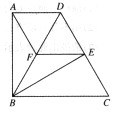
(1)求证:AD=ED;
(2)如果AF∥CD,求证:四边形ADEF是菱形.
(本小题满分l0分)如图所示(左图为实景侧视图,右图为安装示意图),在屋顶的斜坡面上安装太阳能热水器:先安装支架AB和CD(均与水平面垂直),再将集热板安装在AD上.为使集热板吸热率更高,公司规定:AD与水平线夹角为θ1,且在水平线上的射影AF为140cm.现已测量出屋顶斜面与水平面夹角为θ2,并已知tanθ1≈1.1,tanθ2≈0.4.如果安装工人已确定支架加高为25 cm,求支架CD的高(结果精确到1 cm)?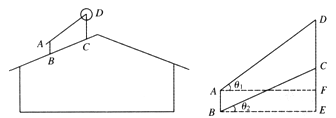
(本小题满分8分)某初级中学准备随机选出七、八、九三个年级各1名学生担任领操员.现已知这三 个年级分别选送一男、一女共6名学生为备选人.请你利用树状图或表格求选出“两男一女”三名领操员的概率.