(本小题满分12分) 如图所示,等腰△ABC的底边AB= ,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记BE=x,V(x)表示四棱锥P-ACFE的体积.
,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记BE=x,V(x)表示四棱锥P-ACFE的体积.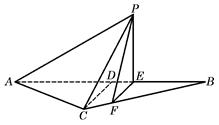
(Ⅰ)求V(x)的表达式;
(Ⅱ)当x为何值时,V(x)取得最大值?
已知二次函数 的最小值为
的最小值为 且关于
且关于 的不等式
的不等式 的解集为
的解集为 ,
,
(1)求函数 的解析式;
的解析式;
(2)求函数 的零点个数.
的零点个数.
如图,四棱柱 的底面
的底面 是平行四边形,
是平行四边形, 分别在棱
分别在棱 上,且
上,且 .
.
(1)求证: ;
;
(2)若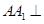 平面
平面 ,四边形
,四边形 是边长为
是边长为 的正方形,且
的正方形,且 ,
, ,求线段
,求线段 的长, 并证明:
的长, 并证明:

设函数 ,其中
,其中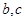 是某范围内的随机数,分别在下列条件下,求事件A “
是某范围内的随机数,分别在下列条件下,求事件A “ 且
且 ”发生的概率.
”发生的概率.
(1) 若随机数 ;
;
(2) 已知随机函数 产生的随机数的范围为
产生的随机数的范围为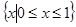 ,
, 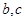 是算法语句
是算法语句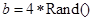 和
和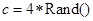 的执行结果.(注: 符号“
的执行结果.(注: 符号“ ”表示“乘号”)
”表示“乘号”)
在 中,角
中,角 为锐角,记角
为锐角,记角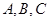 所对的边分别为
所对的边分别为 设向量
设向量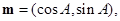
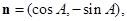 且
且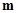 与
与 的夹角为
的夹角为
(1)求 的值及角
的值及角 的大小;
的大小;
(2)若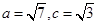 ,求
,求 的面积
的面积 .
.
已知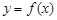 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, .
.
(1)求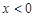 时,
时, 的解析式;
的解析式;
(2)问是否存在这样的非负数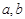 ,当
,当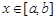 时,
时, 的值域为
的值域为 ?若存在,求出所有的
?若存在,求出所有的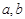 值;若不存在,请说明理由.
值;若不存在,请说明理由.