如图所示, ,
, ,
, ,点
,点 是以
是以 为直径的半圆
为直径的半圆 上一动点,
上一动点, 交直线
交直线 于点
于点 ,设
,设 .
.当
 时,求
时,求 的长;
的长;当
 时,求线段
时,求线段 的长;
的长;若要使点
 在线段
在线段 的延长线上,则
的延长线上,则 的取值范围是_______.(直接写出答案)
的取值范围是_______.(直接写出答案)
某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表.
根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图;
(2)扇形统计图中“C组”所对应的圆心角的度数是 ;
(3)已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.
化简:(1+ )÷
)÷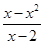 .
.
(1)计算:(-2)2+( -π)0+|1-
-π)0+|1- |;
|;
(2)解方程组: .
.
如图,抛物线 与x轴交于点A、B两点,与y轴交于点C,且A点坐标(-3,0),连接BC、AC.
与x轴交于点A、B两点,与y轴交于点C,且A点坐标(-3,0),连接BC、AC.
(1)求该抛物线解析式;
(2)求AB和OC的长;
(3)点E从点B出发,沿x轴向点A运动(点E与点A、B不重合),过点E作直线l平行AC,交BC于点D,设BE的长为m,△BDE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(4)在(3)的条件下,连接CE,求△CDE面积的最大值.
如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M是直线CD上异于点C、O、D的一个动点,AM所在的直线交于⊙O于点N,点P是直线CD上另一点,且PM=PN.
(1)当点M在⊙O内部,如图一,试判断PN与⊙O的关系,并写出证明过程;
(2)当点M在⊙O外部,如图二,其它条件不变时,(1)的结论是否成立?请说明理由;
(3)当点M在⊙O外部,如图三,∠AMO=30°,求图中阴影部分的面积.