知识迁移
当
且
时，因为
≥
,所以
≥,从而
≥
(当
时取等号).
记函数
,由上述结论可知：当时,该函数有最小值为
直接应用
已知函数
与函数
, 则当
____时,
取得最小值为___.
变形应用
已知函数
与函数
,求
的最小值,并指出取得
该最小值时相应的
的值.
实际应用
已知某汽车的一次运输成本包含以下三个部分：一是固定费用,共
元；二是燃油费,每千
米为
元；三是折旧费,它与路程的平方成正比,比例系数为
.设该汽车一次运输的路
程为
千米,求当为多少时,该汽车平均每千米的运输成本最低？最低是多少元？
如图，点A、B、C、D在⊙O上，∠ADC=60°，C是弧AB的中点．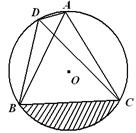
（1）判断△ABC的形状，并说明理由；
（2）若BC=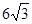
cm，求图中阴影部分的面积．
市体育协会在天德湖公园主办的放风筝比赛. 比赛中小军在A处不小心让风筝挂在了一棵树的树梢上（如图），固定在了D处，此时风筝线AD与水平线的夹角为30°. 为了便于观察，小军迅速向前边移动边收线到达了离A处6米的B处，此时风筝线BD与水平线的夹角为45°. 已知点A、B、C在同一条直线上，∠ACD=90°. 请求出此时小军手中的风筝线BD的长度约是多少米？（本题中风筝线均视为线段，
，
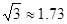，最后结果精确到1米）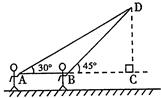
如图，在□ABCD中，∠ABD的平分线BE交AD于点E，∠CDB的平分线DF交BC于点F，连接BD．
（1）求证：△ABE≌△CDF；
（2）若AB＝DB，求证：四边形DFBE是矩形．
为增强环保意识，某社区计划开展一次“低碳环保，绿色出行”的宣传活动，对部分家庭四月份平均每天用车的时间进行了一次抽样调查，并根据收集的数据绘制了下面两幅不完整的统计图．请根据图中提供的信息，解答下列问题：
（1）本次抽样调查了多少个家庭？
（2）将图1中的条形图补充完整，直接写出用车时间的中位数落在哪个时间段内；
（3）求用车时间在1～1.5小时的部分对应的扇形圆心角的度数；
（4）若该社区有车家庭有1200个，请你估计该社区用车时间不超过1.5小时的约有多少个家庭？
小明和小刚做游戏，用一个不透明袋子，里面装有形状、大小完全相同的2个红球和２个白球，并充分搅匀，让小刚从中摸出一个球不放回，再去摸第二个球，如果两次摸出的球颜色相同小刚赢，反之小明赢. 你认为这种游戏是否公平？请你借助树状图或列表的方法，运用概率的知识予以说明．