在平面直角坐标系 中,已知二次函数
中,已知二次函数 的图象经过点
的图象经过点 和点
和点 ,直线
,直线 经过抛物线的顶点且与
经过抛物线的顶点且与 轴垂直,垂足为
轴垂直,垂足为 .
.求该二次函数的表达式;
设抛物线上有一动点
 从点
从点 处出发沿抛物线向上运动,其纵坐标
处出发沿抛物线向上运动,其纵坐标 随时间
随时间 ≥
≥ )的变化规律为
)的变化规律为 .现以线段
.现以线段 为直径作
为直径作 .
.
①当点 在起始位置点
在起始位置点 处时,试判断直线
处时,试判断直线 与
与 的位置关系,并说明理由;在点
的位置关系,并说明理由;在点 运动的过程中,直线
运动的过程中,直线 与
与 是否始终保持这种位置关系? 请说明你的理由;
是否始终保持这种位置关系? 请说明你的理由;
②若在点 开始运动的同时,直线
开始运动的同时,直线 也向上平行移动,且垂足
也向上平行移动,且垂足 的纵坐标
的纵坐标 随时间
随时间 的变化规律为
的变化规律为 ,则当
,则当 在什么范围内变化时,直线
在什么范围内变化时,直线 与
与 相交? 此时,若直线
相交? 此时,若直线 被
被 所截得的弦长为
所截得的弦长为 ,试求
,试求 的最大值.
的最大值.
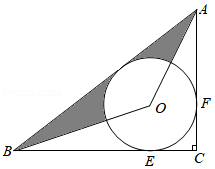
如图,在 中, , 与 , 分别相切于点 , , 平分 ,连接 .
(1)求证: 是 的切线;
(2)若 , 的半径是1,求图中阴影部分的面积.
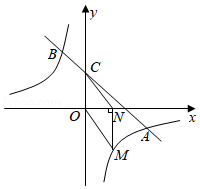
如图,反比例函数 的图象与一次函数 的图象相交于 , 两点.
(1)求反比例函数和一次函数的解析式;
(2)设直线 交 轴于点 ,点 是 轴正半轴上的一个动点,过点 作 轴交反比例函数 的图象于点 ,连接 , .若 ,求 的取值范围.
2021年,黄冈、咸宁、孝感三市实行中考联合命题,为确保联合命题的公平性,决定采取三轮抽签的方式来确定各市选派命题组长的学科.第一轮,各市从语文、数学、英语三个学科中随机抽取一科;第二轮,各市从物理、化学、历史三个学科中随机抽取一科;第三轮,各市从道德与法治、地理、生物三个学科中随机抽取一科.
(1)黄冈在第一轮抽到语文学科的概率是 ;
(2)用画树状图或列表法求黄冈在第二轮和第三轮抽签中,抽到的学科恰好是历史和地理的概率.
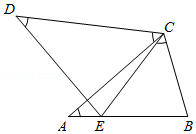
如图,在 和 中, , .
(1)求证: ;
(2)若 , ,求 的长.
计算: .