(本题10分)如图所示,将一矩形花坛 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛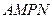 ,要求
,要求 在
在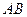 的延长线上,
的延长线上,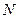 在
在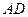 的延长线上,且对角线
的延长线上,且对角线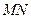 过
过 点.已知
点.已知 米,
米, 米.
米.
(1)设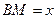 (单位:米),要使花坛
(单位:米),要使花坛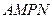 的面积大于9平方米,求
的面积大于9平方米,求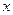 的取值范围;
的取值范围;
(2)若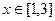 (单位:米),则当
(单位:米),则当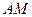 ,
, 的长度分别是多少时,花坛
的长度分别是多少时,花坛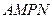 的面积最大?并求出最大面积.
的面积最大?并求出最大面积.
(本题8分)己知集合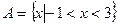 , 集合
, 集合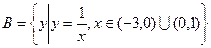 ,
,
集合 .
.
(1)求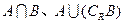 ;
;
(2)若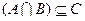 ,求
,求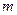 的取值范围.
的取值范围.
如图,在三棱锥 中,已知△
中,已知△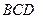 是正三角形,
是正三角形, 平面
平面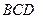 ,
,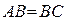 ,
,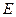 为
为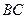 的中点,
的中点, 在棱
在棱 上,且
上,且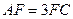 ,
,
(1)求证: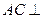 平面
平面 ;
;
(2)求平面 与平面
与平面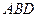 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
(3)若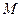 为
为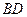 的中点,问
的中点,问 上是否存在一点
上是否存在一点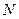 ,使
,使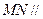 平面
平面 ?若存在,说明点
?若存在,说明点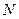 的位置;若不存在,试说明理由.
的位置;若不存在,试说明理由.
如图,矩形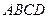 与正三角形
与正三角形 中,
中,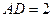 ,
,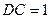 ,
,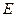 为
为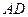 的中点。现将正三角形
的中点。现将正三角形 沿
沿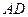 折起,得到四棱锥的三视图如下:
折起,得到四棱锥的三视图如下:
(1)求四棱锥 的体积;
的体积;
(2)求异面直线 所成角的大小。
所成角的大小。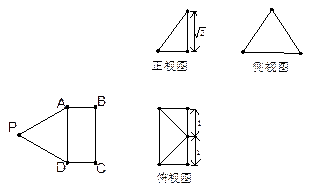
已知直线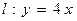 和点
和点 ,点
,点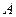 为第一象限内的点且在直线
为第一象限内的点且在直线 上,直线
上,直线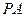 交
交 轴正半轴于点
轴正半轴于点 ,求△
,求△ 面积的最小值,并求当△
面积的最小值,并求当△ 面积取最小值时的
面积取最小值时的 的坐标。
的坐标。