(本小题满分12分)设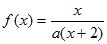 ,方程
,方程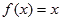 有唯一解,已知
有唯一解,已知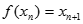
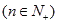 ,且
,且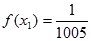 .
.
(Ⅰ)求证:数列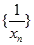 为等差数列,并求数列
为等差数列,并求数列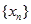 的通项公式;
的通项公式;
(Ⅱ)若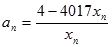 ,且
,且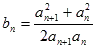
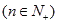 ,求数列
,求数列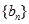 的前
的前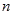 项和
项和 .
.
((本小题满分12分)
已知点 及圆
及圆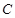 :
: .
.
(1)若直线 过点
过点 且与圆心
且与圆心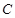 的距离为1,求直线
的距离为1,求直线 的方程;
的方程;
(2)设过点P的直线 与圆
与圆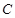 交于
交于 、
、 两点,当
两点,当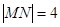 时,求以线段
时,求以线段 为直径的圆
为直径的圆 的方程;
的方程;
(3)设直线 与圆
与圆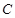 交于
交于 ,
, 两点,是否存在实数
两点,是否存在实数 ,使得过点
,使得过点 的直线
的直线 垂直平分弦
垂直平分弦 ?若存在,求出实数
?若存在,求出实数 的值;若不存在,请说明理由
的值;若不存在,请说明理由
((本小题满分12分)
已知过点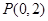 的直线
的直线 与抛物线
与抛物线 交于
交于 、
、 两点,
两点, 为坐标原点.
为坐标原点.
(1)若以 为直径的圆经过原点
为直径的圆经过原点 ,求直线
,求直线 的方程;
的方程;
(2)若线段 的中垂线交
的中垂线交 轴于点
轴于点 ,求
,求 面积的取值范围.
面积的取值范围.
((本小题满分12分)
汽车在道路上行驶每100千米平均燃料消耗量(单位:升)称为百公里油耗.已知某型号汽车在匀速行驶中每小时的耗油量 (升)关于行驶速度
(升)关于行驶速度 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: .
.
(1)当该型号汽车以40千米/小时的速度匀速行驶时,百公里油耗是多少升?
(2)当该型号汽车以多大的速度匀速行驶时,百公里油耗最低?最低为多少升?
((本小题满分12分)
已知函数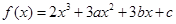 在
在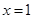 及
及 处取得极值.
处取得极值.
(1)求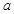 、
、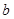 的值;
的值;
(2)若方程 有三个根,求
有三个根,求 的取值范围.
的取值范围.
已知双曲线C: ,
,
(1) 求双曲线C的渐近线方程;
(2) 已知点M的坐标为(0,1).设P是双曲线C上的点,Q是点P关于原点的对称点.记 ,求λ的取值范围;
,求λ的取值范围;
(3) 已知点D、E、M的坐标分别为(-2,-1)、(2,-1)、(0,1),P为双曲线C上在第一象限内的点.记l为经过原点与点P的直线,s为△DEM截直线l所得线段的长.试将s表示为直线l的斜率k的函数.