(本小题满分13分)如图,椭圆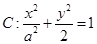 的焦点在
的焦点在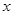 轴上,左、右顶点分别为
轴上,左、右顶点分别为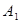 、
、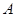 ,上顶点为
,上顶点为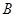 ,抛物线
,抛物线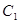 、
、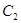 分别以
分别以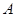 、
、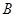 为焦点,其顶点均为坐标原点
为焦点,其顶点均为坐标原点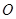 ,
,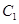 与
与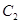 相交于直线
相交于直线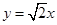 上一点
上一点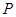 .
.
(Ⅰ)求椭圆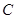 及抛物线
及抛物线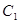 、
、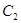 的方程;
的方程;
(Ⅱ)若动直线 与直线
与直线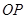 垂直,且与椭圆
垂直,且与椭圆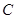 交于不同的两点
交于不同的两点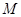 、
、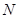 ,已知点
,已知点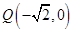 ,求
,求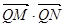 的最小值.
的最小值. 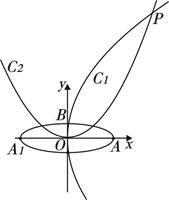
.(本小题满分12分)对于函数 ,若
,若 ,则称
,则称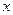 为
为 的“不动点”,若
的“不动点”,若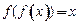 ,则称
,则称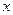 为
为 的“稳定点”.函数的“不动点”和“稳定点”的集合分别记为
的“稳定点”.函数的“不动点”和“稳定点”的集合分别记为 和
和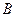 ,即
,即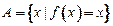 ,
, .
.
(1)求证: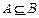 ;
;
(2)若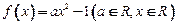 ,且
,且 ,求实数
,求实数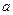 的取值范围;
的取值范围;
(3)若 是
是 上的单调递增函数,
上的单调递增函数,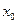 是函数的稳定点,问
是函数的稳定点,问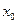 是函数的不动点吗?若是,请证明你的结论;若不是,请说明的理由.
是函数的不动点吗?若是,请证明你的结论;若不是,请说明的理由.
.(本小题满分12分)设函数 的定义域为R,当
的定义域为R,当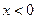 时,
时,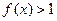 ,且对任意实数
,且对任意实数 ,都有
,都有 成立,数列
成立,数列 满足
满足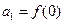 且
且
(1)求 的值;
的值;
(2)若不等式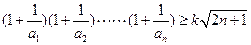 对一切
对一切 均成立,求
均成立,求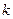 的最大值.
的最大值.
.已知椭圆 过点
过点 ,且离心率e=.
,且离心率e=.
(1)求椭圆方程;
(2)若直线 与椭圆交于不同的两点
与椭圆交于不同的两点 、
、 ,且线段
,且线段 的垂直平分线过定点
的垂直平分线过定点 ,求
,求 的取值范围。
的取值范围。
.(本小题满分12分)如图,在正方体 中,
中, 、
、 分别为棱
分别为棱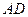 、
、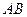 的中点.
的中点.
(1)求证: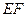 ∥平面
∥平面 ;
;
(2)求证:平面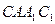 ⊥平面
⊥平面 ;
;
(3)如果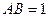 ,一个动点从点
,一个动点从点 出发在正方体的
出发在正方体的
表面上依次经过棱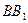 、
、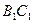 、
、 、
、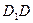 、
、 上的点,最终又回到点
上的点,最终又回到点 ,指出整个路线长度的最小值并说明理由.
,指出整个路线长度的最小值并说明理由.
.(本小题满分12分)已知函数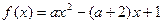 .若
.若 为整数,且函数
为整数,且函数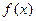 在
在 内恰有一个零点,求
内恰有一个零点,求 的值.
的值.