如图,四棱柱 中,
中,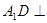 平面
平面 ,底面
,底面 是边长为
是边长为 的正方形,侧棱
的正方形,侧棱 .
.
(1)求三棱锥 的体积;
的体积;
(2)求直线 与平面
与平面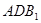 所成角的正弦值;
所成角的正弦值;
(3)若棱 上存在一点
上存在一点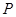 ,使得
,使得 ,当二面角
,当二面角 的大小为
的大小为 时,求实数
时,求实数 的值.
的值.
已知圆C方程:(x-1)2 + y 2=9,垂直于x轴的直线L与圆C相切于N点(N在圆心C的右侧),平面上有一动点P,若PQ⊥L,垂足为Q,且 ;
;
(1)求点P的轨迹方程;
(2)已知D为点P的轨迹曲线上第一象限弧上一点,O为原点,A、B分别为点P的轨迹曲线与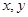 轴的正半轴的交点,求四边形OADB的最大面积及D点坐标.
轴的正半轴的交点,求四边形OADB的最大面积及D点坐标.
已知函数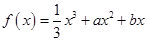
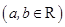 .
.
(1)若曲线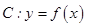 经过点
经过点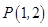 ,曲线
,曲线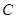 在点
在点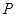 处的切线与直线
处的切线与直线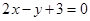 平行,求
平行,求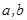 的值;
的值;
(2)在(1)的条件下,试求函数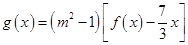 (
(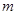 为实常数,
为实常数,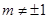 )的极大值与极小值之差;
)的极大值与极小值之差;
在边长为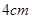 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.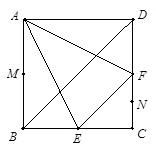
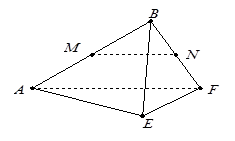
(1)判别MN与平面AEF的位置关系,并给出证明;
(2)证明AB⊥平面BEF;
(3)求多面体E-AFNM的体积.
某学校900名学生在一次百米测试中,成绩全部介于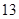 秒与
秒与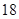 秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组
秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组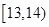 ,第二组
,第二组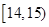 ,…,第五组
,…,第五组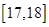 ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.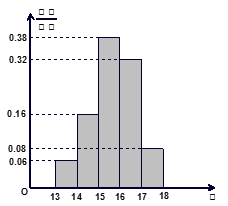
(1)若成绩小于14秒认为优秀,求该样本在这次百米测试中成绩优秀的人数;
(2)请估计本年级900名学生中,成绩属于第三组的人数;
(3)若样本第一组中只有一个女生,其他都是男生,第五组则只有一个男生,其他都是女生,现从第一、五组中各抽一个同学组成一个新的组,求这个新组恰好由一个男生和一个女生构成的概率.
已知函数 的部分图象如图所示.
的部分图象如图所示.
(1)求函数 的解析式,并写出
的解析式,并写出 的单调减区间;
的单调减区间;
(2)记 的内角
的内角 的对边长分别为
的对边长分别为 ,
,
若 ,
, ,
, 求
求 的面积.
的面积.