设点 是抛物线
是抛物线

 的焦点,
的焦点, 是抛物线
是抛物线 上的
上的 个不同的点(
个不同的点(
 ).
).
(1) 当 时,试写出抛物线
时,试写出抛物线 上的三个定点
上的三个定点 、
、 、
、 的坐标,从而使得
的坐标,从而使得 ;
;
(2)当 时,若
时,若 ,
,
求证: ;
;
(3) 当 时,某同学对(2)的逆命题,即:
时,某同学对(2)的逆命题,即:
“若 ,则
,则 .”
.”
开展了研究并发现其为假命题.
请你就此从以下三个研究方向中任选一个开展研究:
① 试构造一个说明该逆命题确实是假命题的反例(本研究方向最高得4分);
② 对任意给定的大于3的正整数 ,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);
,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);
③ 如果补充一个条件后能使该逆命题为真,请写出你认为需要补充的一个条件,并说明加上该条件后,能使该逆命题为真命题的理由(本研究方向最高得10分).
【评分说明】本小题若填空不止一个研究方向,则以实得分最高的一个研究方向的得分作为本小题的最终得分.
已知函数,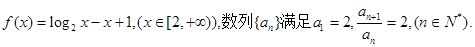
(I)求数列 的通项公式
的通项公式 ;
;
(II)求 ;
;
已知关于x的不等式 (其中
(其中 ).
).
(Ⅰ)当a=4时,求不等式的解集;
(Ⅱ)若不等式有解,求实数a的取值范围.
在极坐标系中,曲线 ,过点A(5,α)(α为锐角且
,过点A(5,α)(α为锐角且 )作平行于
)作平行于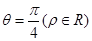 的直线
的直线 ,且
,且 与曲线L分别交于B,C两点.
与曲线L分别交于B,C两点.
(Ⅰ)以极点为原点,极轴为x轴的正半轴,取与极坐标相同单位长度,建立平面直角坐标系,写出曲线L和直线 的普通方程;
的普通方程;
(Ⅱ)求|BC|的长.
如图, 与
与 相交于A、B两点,AB是
相交于A、B两点,AB是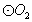 的直径,过A点作
的直径,过A点作 的切线交
的切线交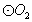 于点E,并与BO1的延长线交于点P,PB分别与
于点E,并与BO1的延长线交于点P,PB分别与 、
、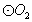 交于C,D两点.
交于C,D两点.
求证:(Ⅰ)PA·PD=PE·PC;
(Ⅱ)AD=AE.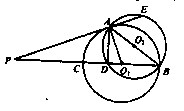
已知函数f(x)=ax+lnx,其中a为常数,设e为自然对数的底数.
(Ⅰ) 当a=-1时,求f(x)的最大值;
(Ⅱ) 若f(x)在区间(0,e]上的最大值为-3,求a的值;
(Ⅲ) 当a=-1时,试推断方程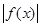 =
=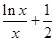 是否有实数解.
是否有实数解.