已知数列 是各项均不为0的等差数列,公差为d,
是各项均不为0的等差数列,公差为d,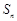 为其前n项和,且满足
为其前n项和,且满足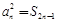 ,
,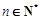 .数列
.数列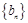 满足
满足 ,
,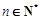 ,
, 为数列
为数列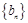 的前n项和.
的前n项和.
(1)求数列 的通项公式
的通项公式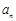 和数列
和数列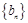 的前n项和
的前n项和 ;
;
(2)若对任意的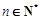 ,不等式
,不等式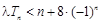 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)是否存在正整数
 ,使得
,使得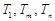 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分10分)选修4—4:坐标系与参数方程
在以坐标原点为极点, 轴的正半轴为极轴建立的极坐标系中,曲线
轴的正半轴为极轴建立的极坐标系中,曲线 的极坐标方程为
的极坐标方程为 ,正三角形
,正三角形 的顶点都在
的顶点都在 上,且
上,且 ,
, ,
, 依逆时针次序排列,点
依逆时针次序排列,点 的坐标为
的坐标为 .
.
(1)求点 ,
, 的直角坐标系;
的直角坐标系;
(2)设 是圆
是圆 :
: 上的任意一点,求
上的任意一点,求 的取值范围.
的取值范围.
(本小题满分10分)选修4—1:几何证明选讲
如图所示,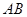 是
是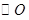 的直径,
的直径,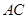 切
切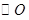 于点
于点 ,
, ,
,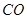 交
交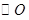 于点
于点 ,
,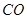 的延长线交
的延长线交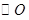 于点
于点 ,
, 的延长线交
的延长线交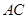 于点
于点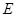 .
.
(1)求证: ;
;
(2)若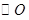 的直径
的直径 ,求
,求 的值.
的值.
(本小题满分12分)设函数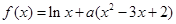 ,其中
,其中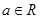 .
.
(1)讨论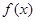 极值点的个数;
极值点的个数;
(2)设 ,函数
,函数 ,若
,若 ,
, (
( )满足
)满足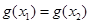 且
且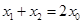 ,证明:
,证明: .
.
(本小题满分12分)已知椭圆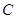 :
: 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切.
(1)求椭圆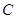 的方程;
的方程;
(2)设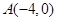 ,过点
,过点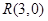 作与
作与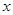 轴不重合的直线
轴不重合的直线 交椭圆
交椭圆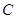 于
于 ,
,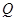 两点,连接
两点,连接 ,
, 分别交直线
分别交直线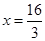 于
于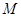 ,
, 两点,若直线
两点,若直线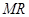 、
、 的斜率分别为
的斜率分别为 、
、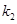 ,试问:
,试问: 是否为定值?若是,求出该定值,若不是,请说明理由.
是否为定值?若是,求出该定值,若不是,请说明理由.
(本小题满分12分)某商家对他所经销的一种商品的日销售量(单位:吨)进行统计,最近50天的统计结果如下表:
| 日销售量 |
1 |
1.5 |
2 |
| 天数 |
10 |
25 |
15 |
| 频率 |
 |
 |
 |
若以上表中频率作为概率,且每天的销售量相互独立.
(1)求5天中该种商品恰好有两天的销售量为1.5吨的概率;
(2)已知每顿该商品的销售利润为2千元, 表示该种商品某两天销售利润的和(单位:千元),求
表示该种商品某两天销售利润的和(单位:千元),求 的分布列和数学期望.
的分布列和数学期望.