(本小题满分12分)如图: 、
、 是以
是以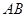 为直径的圆上两点,
为直径的圆上两点,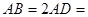
 ,
,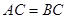 ,
, 是
是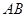 上一点,且
上一点,且 ,将圆沿直径
,将圆沿直径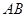 折起,使点
折起,使点 在平面
在平面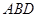 的射影
的射影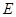 在
在 上.
上.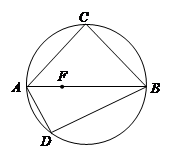
(1)求证: 平面
平面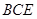 ;
;
(2)求证: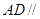 平面
平面 ;
;
(3)求三棱锥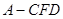 的体积.
的体积.
(本小题满分14分)等比数列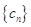 满足
满足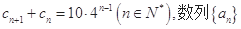 的前n项和为
的前n项和为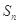 ,且
,且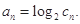
(1)求 ;
;
(2)数列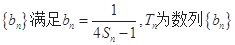 的前n项和,是否存在正整数m,
的前n项和,是否存在正整数m,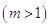 ,使得
,使得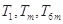 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有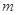 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分14分)如图,斜三棱柱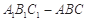 中,侧面
中,侧面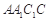
 底面ABC,底面ABC是边长为2的等边三角形,侧面
底面ABC,底面ABC是边长为2的等边三角形,侧面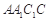 是菱形,
是菱形,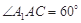 ,E、F分别是
,E、F分别是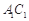 、AB的中点.
、AB的中点.
求证:(Ⅰ) ;
;
(Ⅱ)求三棱锥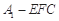 的体积.
的体积.
(本小题满分12分)为了宣传今年10月在某市举行的“第十届中国艺术节”, “十艺节”筹委会举办了“十艺节”知识有奖问答活动,随机对市民15~65岁的人群抽样n人,回答问题统计结果如下图表所示:
(Ⅰ)分别求出a,x的值;
(Ⅱ)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,“十艺节”筹委会决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率.
(本小题满分12分)已知函数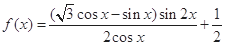 .
.
(1)求 的值;
的值;
(2)求函数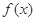 的最小正周期及单调递减区间.
的最小正周期及单调递减区间.
已知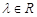 ,函数
,函数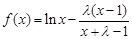 ,其中
,其中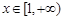 .
.
(Ⅰ)当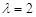 时,求
时,求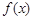 的最小值;
的最小值;
(Ⅱ)在函数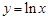 的图像上取点
的图像上取点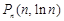
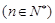 ,记线段PnPn+1的斜率为kn ,
,记线段PnPn+1的斜率为kn ,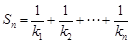 .对任意正整数n,试证明:
.对任意正整数n,试证明:
(ⅰ)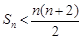 ;
;
(ⅱ)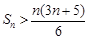 .
.