操作:小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的圆形纸片进行如下设计:
纸片利用率= ×100%
×100%
发现:(1)方案一中的点A、B恰好为该圆一直径的两个端点.
你认为小明的这个发现是否正确,请说明理由.
(2)小明通过计算,发现方案一中纸片的利用率仅约为38.2%.
请帮忙计算方案二的利用率,并写出求解过程.
探究:(3)小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.

某校开展“中国梦•泉州梦•我的梦”主题教育系列活动,设有征文、独唱、绘画、手抄报四个项目,该校共有800人次参加活动.下面是该校根据参加人次绘制的两幅不完整的统计图,请根据图中提供的信息,解答下面的问题.
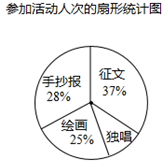
(1)此次有 名同学参加绘画活动,扇形统计图中“独唱”部分的圆心角是 度.请你把条形统计图补充完整.
(2)经研究,决定拨给各项目活动经费,标准是:征文、独唱、绘画、手抄报每人次分别为10元、12元、15元、12元,请你帮学校计算开展本次活动共需多少经费?
已知抛物线y=a(x﹣3)2+2经过点(1,﹣2).
(1)求a的值;
(2)若点A(m,y1)、B(n,y2)(m<n<3)都在该抛物线上,试比较y1与y2的大小.
四张小卡片上分别写有数字1、2、3、4,它们除数字外没有任何区别,现将它们放在盒子里搅匀.
(1)随机地从盒子里抽取一张,求抽到数字3的概率;
(2)随机地从盒子里抽取一张,将数字记为x,不放回再抽取第二张,将数字记为y,请你用画树状图或列表的方法表示所有等可能的结果,并求出点(x,y)在函数 图象上的概率.
图象上的概率.
如图,已知AD是△ABC的中线,分别过点B、C作BE⊥AD于点E,CF⊥AD交AD的延长线于点F,求证:BE=CF.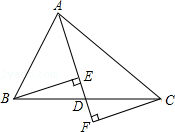
先化简,再求值:(x﹣1)2+x(x+2),其中x=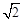 .
.