(本小题满分15分)已知函数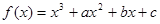 ,曲线
,曲线 在点
在点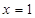 处的切线为
处的切线为 若
若 时,
时, 有极值.
有极值.
(1)求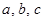 的值;
的值;
(2)求 在
在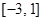 上的最大值和最小值.
上的最大值和最小值.
甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
| 优秀 |
非优秀 |
总计 |
|
| 甲班 |
10 |
||
| 乙班 |
30 |
||
| 合计 |
105 |
已知在全部105人中抽到随机抽取1人为优秀的概率为
(Ⅰ)请完成上面的列联表;
(Ⅱ)根据列联表的数据,若按 的可靠性要求,能否认为“成绩与班级有关系” .
的可靠性要求,能否认为“成绩与班级有关系” .
(Ⅲ)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到6或10号的概率.
参考公式: 

在△ABC中,角A、B、C的对边分别为a、b、c,若
(Ⅰ)求证:A=B;
(Ⅱ)求边长c的值;
(Ⅲ)若 求△ABC的面积.
求△ABC的面积.
已知函数 ,其中
,其中 。
。
(1)求函数 的单调区间;
的单调区间;
(2)若直线 是曲线
是曲线 的切线,求实数
的切线,求实数 的值;
的值;
(3)设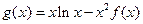 ,求
,求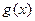 在区间
在区间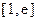 上的最大值(其
上的最大值(其 中
中 为自然对数的底数)。
为自然对数的底数)。
如图所示,设椭圆C1: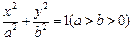 的左、右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点),如图。若抛物线C2:
的左、右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点),如图。若抛物线C2: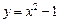 与y轴的交点为B,且经过F1,F2点
与y轴的交点为B,且经过F1,F2点
(1 )求椭圆C1的方程;
)求椭圆C1的方程;
(2)设M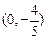 ),N为抛物线C2上的一动点,过点N作抛物线C2的切线交椭圆C1于P、Q两点,求
),N为抛物线C2上的一动点,过点N作抛物线C2的切线交椭圆C1于P、Q两点,求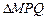 面积的最大值。
面积的最大值。
已知函数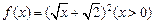 ,设正项数列
,设正项数列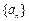 的首项
的首项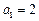 ,前n 项和
,前n 项和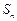 满足
满足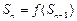 (
(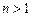 ,且
,且 )。
)。
(1)求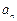 的表达式;
的表达式;
(2)在平面直角坐标系内,直线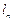 的斜率为
的斜率为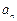 ,且
,且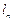 与曲线
与曲线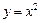 相切,
相切,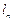 又与y轴交于点
又与y轴交于点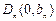 ,当
,当 时,记
时,记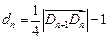 ,若
,若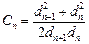 ,求数列
,求数列 的前n 项和
的前n 项和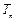 。
。