甲、乙两公司生产同一种新产品,经测算,对于函数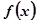 、
、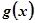 及任意的
及任意的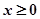 ,当甲公司投入
,当甲公司投入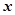 万元作宣传时,若乙公司投入的宣传费小于
万元作宣传时,若乙公司投入的宣传费小于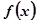 万元,则乙公司有失败的风险,否则无失败的风险;当乙公司投入
万元,则乙公司有失败的风险,否则无失败的风险;当乙公司投入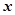 万元作宣传时,若甲公司投入的宣传费小于
万元作宣传时,若甲公司投入的宣传费小于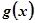 万元,则甲公司有失败的风险,否则无失败的风险.
万元,则甲公司有失败的风险,否则无失败的风险.
(1)请解释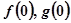 的实际意义;
的实际意义;
(2)当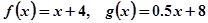 时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能地少投入宣传费用,问此时甲、乙两公司应各投入多少宣传费用?
时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能地少投入宣传费用,问此时甲、乙两公司应各投入多少宣传费用?
某工厂某种航空产品的年固定成本为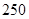 万元,每生产
万元,每生产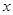 件,需另投入成本为
件,需另投入成本为 ,当年产量不足
,当年产量不足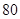 件时,
件时,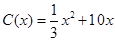 (万元).当年产量不小于
(万元).当年产量不小于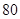 件时,
件时,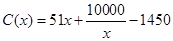 (万元).每件商品售价为
(万元).每件商品售价为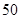 万元.通过市场分析,该厂生产的商品能全部售完.
万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润 (万元)关于年产量
(万元)关于年产量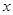 (件)的函数解析式;
(件)的函数解析式;
(2)年产量为多少件时,该厂在这一商品的生产中所获利润最大?
已知不等式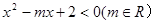 的解集为
的解集为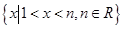 ,函数
,函数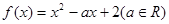 .
.
(1)求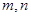 的值;
的值;
(2)若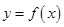 在
在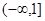 上单调递减,解关于
上单调递减,解关于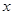 的不等式
的不等式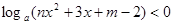 .
.
解不等式组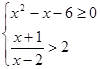 .
.
(本小题满分10分)已知函数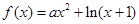
(1)若函数 在区间
在区间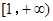 上为减函数,求实数
上为减函数,求实数 的取值范围
的取值范围
(2)当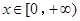 时,不等式
时,不等式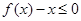 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
(本小题满分10分)已知椭圆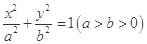 的两个焦点为
的两个焦点为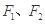 ,离心率为
,离心率为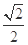 ,直线l与椭圆相交于A、B两点,且满足
,直线l与椭圆相交于A、B两点,且满足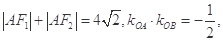
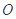 为坐标原点.
为坐标原点.
(1)求椭圆的方程;
(2)证明: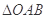 的面积为定值.
的面积为定值.