某农场去年计划生产玉米和小麦共200吨,采用新技术后,实际产量为225吨,其中玉米超产 ,小麦超产 ,该农场去年实际生产玉米、小麦各多少吨?
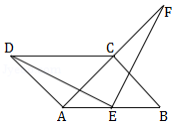
如图,四边形 是平行四边形, , , 是 的中点, 是 延长线上一点.
(1)若 ,求证: ;
(2)在(1)的条件下,若 的延长线与 交于点 ,试判定四边形 是否为平行四边形?并证明你的结论(请先补全图形,再解答);
(3)若 , 与 垂直吗?若垂直给出证明,若不垂直说明理由.
如图,是将抛物线 平移后得到的抛物线,其对称轴为 ,与 轴的一个交点为 ,另一个交点为 ,与 轴的交点为 .
(1)求抛物线的函数表达式;
(2)若点 为抛物线上一点,且 ,求点 的坐标;
(3)点 是抛物线上一点,点 是一次函数 的图象上一点,若四边形 为平行四边形,这样的点 、 是否存在?若存在,分别求出点 、 的坐标;若不存在,说明理由.

如图,四边形 中, , 平分 ,点 是 延长线上一点,且 .
(1)证明: ;
(2)若 与 相交于点 , , ,求 的长.

某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了 .若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的 ,大樱桃的售价最少应为多少?