如图，在△ABC，AB=AC，以AB为直径的⊙O分别交AC、BC于点D、E，点F在
AC的延长线上，且∠CBF=
∠CAB．
（Ⅰ）求证：直线BF是⊙O的切线；
（Ⅱ）若AB=5，sin∠CBF=
，求BC和BF的长．
已知
、
互为相反数，
、
互为倒数，
，求：
的值．
计算：
（1）
（2）
如图，点O是等边△ABC内一点．将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．已知∠AOB=110°．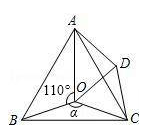
（1）求证：△COD是等边三角形；
（2）当α=150°时，试判断△AOD的形状，并说明理由；
（3）探究：当α为多少度时，△AOD是等腰三角形．
阅读材料：若m2-2mn+2n2-8n+16=0，求m、n的值．
解：∵m2-2mn+2n2-8n+16=0，
∴（m2-2mn+n2）+（n2-8n+16）=0
∴（m-n）2+（n-4）2=0，∴（m-n）2=0，（n-4）2=0，∴n=4，m=4．
根据你的观察，探究下面的问题：
（1）已知x2-2xy+2y2+6y+9=0，求xy的值；
（2）已知△ABC的三边长a、b、c都是正整数，且满足a2+b2-10a-12b+61=0，求△ABC的最大边c的值．
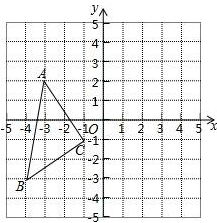
如图，已知△ABC各顶点的坐标分别为A（-3，2），请你画出△ABC关于y轴对称的△A1B1C1，并写出△A1B1C1的各顶点坐标．